Phần câu hỏi bài 2 trang 43, 44 Vở bài tập toán 9 tập 2

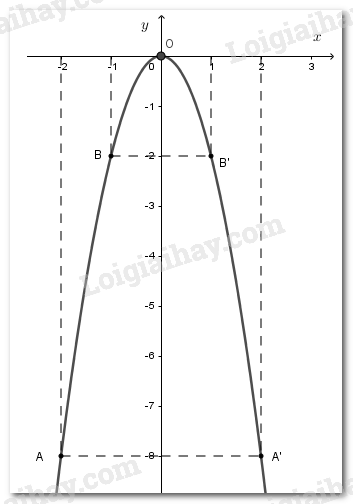
Câu 5

Cho hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\). Khoanh tròn vào chữ cái đặt trước câu đúng.

(A) Đồ thị của hàm số là một đường thẳng đi qua gốc tọa độ

(B) Đồ thị của hàm số là một đường thẳng nhận trục Oy làm trục đối xứng

(C) Đồ thị của hàm số là một đường cong nhận Oy làm trục đối xứng và đi qua gốc tọa độ.

(D) Nếu một đường cong nhận Oy làm trục đối xứng và đi qua gốc tọa độ thì đó là đồ thị hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\)

Phương pháp giải:

Sử dụng kiến thức về đồ thị hàm số \(y = a{x^2}\,\left( {a \ne 0} \right)\) 

Lời giải chi tiết:

Đồ thị của hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) là một đường cong đi qua gốc tọa độ \(O\) và nhận trục \(Oy\) làm trục đối xứng.

Chọn C.

Câu 6

Cho hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\). Khoanh tròn vào chữ cái đặt trước câu đúng.

(A) Đồ thị của hàm số luôn luôn nằm phía trên trục Ox

(B) Mọi điểm của đồ thị hàm số đều không nằm trên trục hoành.

(C) Nếu a > 0 thì đồ thị hàm số nằm phía dưới trục hoành

(D) Với mọi \(a \ne 0\) có một điểm duy nhất của đồ thị hàm số thuộc trục hoành

Phương pháp giải:

Sử dụng kiến thức về đồ thị hàm số \(y = a{x^2}\,\left( {a \ne 0} \right)\)

Đồ thị của hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) là một đường cong đi qua gốc tọa độ \(O\) và nhận trục \(Oy\) làm trục đối xứng. Đường cong đó là một parabol với đỉnh \(O\).

- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, O  là điểm thấp nhất của đồ thị.

- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, O  là điểm cao nhất của đồ thị.

Lời giải chi tiết:

A sai vì đồ thị hàm số nằm dưới trục \(Ox\) nếu \(a < 0.\)

B sai vì đồ thị hàm số luôn đi qua gốc tọa độ \(O\left( {0;0} \right)\) thuộc trục hoành

C sai vì với \(a > 0\) thì đồ thị hàm số nằm trên trục hoành

D đúng vì đồ thị hàm số luôn đi qua gốc tọa độ \(O\left( {0;0} \right)\) thuộc trục hoành với mọi \(a \ne 0.\)

Chọn D.

Câu 7

Cho hàm số \(y =  - 2{x^2}\) . Các điểm (A(-2 ; -8); B(-1 ; -2); O(0 ; 0); B’(1 ; -2); A’(2 ; -8) thuộc đồ thị của hàm số. Khoanh tròn vào chữ cúa đặt trước cách vẽ đồ thị đúng.

(A) Nối A với A’, B với B’, B’ với O

(B) Nối A với B, B với O, O với A’, A’ với B’.

(C) Nối A với B, B với O, O với B’, B’ với A’.

(D) nối A với O, O với B, B với B’, B’ với A’.

Phương pháp giải:

Dựa vào cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Bước 1: Lập bảng giá trị đặc biệt tương ứng giữa \(x\) và \(y\) của hàm số \(y = {\rm{a}}{{\rm{x}}^2}\,\,(a \ne 0)\).

Bước 2: Biểu diễn các điểm đặc biệt trên mặt phẳng tọa độ và vẽ đồ thị dạng parabol của hàm số đi qua các điểm đặc biệt đó.

 Nhận thấy rằng đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) có hình dạng là một đường cong parabol nên khi ta vẽ đồ thị hàm số thì nối các điểm ở mỗi phía của trục tung với nhau để tạo thành một đường cong trơn.

Lời giải chi tiết:

Đồ thị hàm số \(y =  - 2{x^2}\)

Ta nối các điểm A với B, B với O, O với \(A'\) , \(A'\) với \(B'\)  để được đồ thị hàm số \(y =  - 2{x^2}.\)

Chọn B.

Câu 8

Khoanh tròn vào chữ cái đặt trước câu đúng.

(A) Hàm số \(y = \sqrt {10000} {x^2}\) có giá trị lớn nhất là 100

(B) Hàm số \(y =  - 1230{x^2}\) có giá trị lớn nhất là 0

(C) Hàm số \(y = 2009{x^2}\) không có giá trị nhỏ nhất

(D) Hàm số \(y =  - 0,01{x^2}\) không có giá trị lớn nhất.

Phương pháp giải:

Ta sử dụng

+) Nếu \(a > 0\) thì \(y > 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\). Giá trị nhỏ nhất của hàm số là \(y = 0\).

+) Nếu \(a < 0\) thì \(y < 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\). Giá trị lớn nhất của hàm số là \(y = 0\).

Lời giải chi tiết:

Hàm số \(y =  - 1230{x^2}\) có \(a =  - 1230 < 0\)  nên giá trị lớn nhất của nó là \(0 \Leftrightarrow x = 0.\)

Chọn B.

Loigiaihay.com