Bài 6 trang 154 SGK Đại số 10Tính sina và cosa. Quảng cáo
Đề bài Cho \(\displaystyle \sin 2a = - {5 \over 9}\) và \(\displaystyle {\pi \over 2} < a < π\). Tính \(\displaystyle \sin a\) và \(\displaystyle \cos a.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Với \(\dfrac{{\pi }}{2} < a < \pi\) ta có \(\sin a > 0, \, \, \cos a < 0.\) +) \(\sin^2 \alpha +\cos^2 \alpha =1. \) +) \(\sin 2a = 2\sin a.\cos a.\) +) \(\cos 2a = {\cos ^2}a - {\sin ^2}a \) \(= 2{\cos ^2}a - 1\)\( = 1 - 2{\sin ^2}a.\) +) \(\sin^2 a = \dfrac{{1 - \cos 2a}}{2}.\) +) \(\cos^2 a = \dfrac{{1 + \cos 2a}}{2}.\) Lời giải chi tiết Với \(\displaystyle {\pi \over 2}< a < π\Rightarrow \sin a > 0, \cos a < 0.\) \(\displaystyle \begin{array}{l} Nếu \(\displaystyle \cos 2a = {{2\sqrt {14} } \over 9}\) thì \(\displaystyle {\sin ^2}a = \frac{{1 - \cos 2a}}{2}\) \(\displaystyle \eqalign{ \(\displaystyle {\cos ^2}a = \frac{{1 + \cos 2a}}{2}\) \(\displaystyle \Rightarrow \cos a = - \sqrt {{{1 + \cos 2a} \over 2}} \) \(\displaystyle = - \sqrt {\frac{{1 + \frac{{2\sqrt {14} }}{9}}}{2}} \) \(\displaystyle = - \sqrt {\frac{{9 + 2\sqrt {14} }}{{18}}} \) \(\displaystyle = - \frac{{\sqrt {{{\left( {\sqrt 7 + \sqrt 2 } \right)}^2}} }}{{\sqrt {18} }}\) \(\displaystyle = - \frac{{\sqrt 7 + \sqrt 2 }}{{3\sqrt 2 }} \) \(\displaystyle = - \frac{{\sqrt {14} + 2}}{6}\) Nếu \(\displaystyle \cos 2a = -{{2\sqrt {14} } \over 9}\) thì \(\displaystyle {\sin ^2}a = \frac{{1 - \cos 2a}}{2}\) \(\displaystyle \eqalign{ \(\displaystyle {\cos ^2}a = \frac{{1 + \cos 2a}}{2}\) \(\displaystyle \Rightarrow \cos a = - \sqrt {{{1 + \cos 2a} \over 2}} \) \(\displaystyle = - \sqrt {\frac{{1 - \frac{{2\sqrt {14} }}{9}}}{2}} \) \(\displaystyle = - \sqrt {\frac{{9 - 2\sqrt {14} }}{{18}}} \) \(\displaystyle = - \frac{{\sqrt {{{\left( {\sqrt 7 - \sqrt 2 } \right)}^2}} }}{{\sqrt {18} }}\) \(\displaystyle = - \frac{{\sqrt 7 - \sqrt 2 }}{{3\sqrt 2 }} \) \(\displaystyle = - \frac{{\sqrt {14} - 2}}{6}\) Cách khác: Loigiaihay.com
|














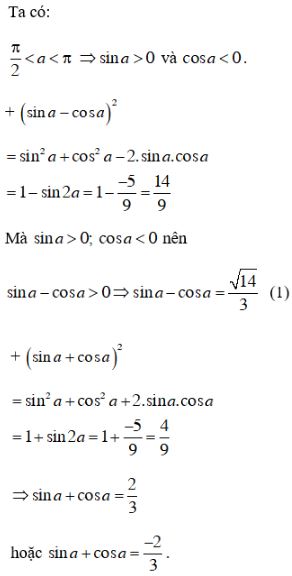







Danh sách bình luận