Bài 58 trang 83 SGK Toán 7 tập 2

Đề bài

Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ngoài tam giác.

Lời giải chi tiết

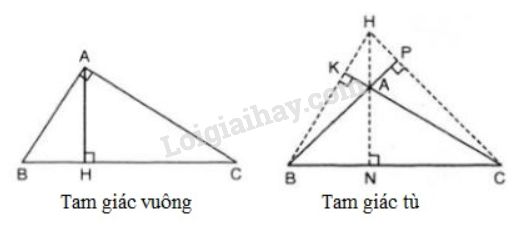
- Trường hợp tam giác \(ABC\) vuông tại \(A\) (hình vẽ) 

+) Xét tam giác \(ABC\) vuông tại \(A\) thì \(BA ⊥ CA\) hay \(AB\) là đường cao ứng với cạnh \(AC\) và \(AC\) là đường cao ứng với cạnh \(AB\)

Do đó, \(AB, AC\) là hai đường cao của tam giác \(ABC\) và \(A\) là giao điểm của hai đường cao \(AB\) và \(AC\)

\( \Rightarrow\) \(A\) là trực tâm của tam giác.

Vậy trong tam giác vuông thì trực tâm trùng với đỉnh góc vuông.

+) Trường hợp tam giác \(ABC\) có góc A là góc tù, các đường cao \(BK, CP\) và \(AN\) ứng với các cạnh \(AC, AB,BC,\) gọi \(H\) là giao điểm của \(BK\) và \(CP\) (hình vẽ) 

 Giả sử \(P\) nằm giữa \(A\) và \(B\), khi đó

\(\widehat {CAP} \equiv \widehat {CAB}\) là góc tù

Xét \(\Delta ACP\) có \(\widehat {CAP}\) tù (\(\widehat {CAP}>90^0)\); \(\widehat {CPA} = {90^o}\)

Suy ra: \(\widehat {CPA} + \widehat {CAP} > 90^0+90^0\)

Hay  \(\widehat {CPA} + \widehat {CAP} >{180^o}\) (mâu thuẫn với định lí tổng \(3\) góc trong một tam giác)

Do đó \(P\) nằm ngoài \(A\) và \(B\). 

\(⇒\) tia \(CP\) nằm ngoài tia \(CA\) và tia \(CB\)

\(⇒\) tia \(CP\) nằm bên ngoài \(ΔABC.\)

Tương tự ta có tia \(BK\) nằm bên ngoài \(ΔABC.\)

Trực tâm \(H\) là giao của \(BK\) và \(CP ⇒ H\) nằm bên ngoài \(ΔABC.\)

Vậy trực tâm của tam giác tù nằm ở bên ngoài tam giác.

Loigiaihay.com