Bài 60 trang 83 SGK Toán 7 tập 2

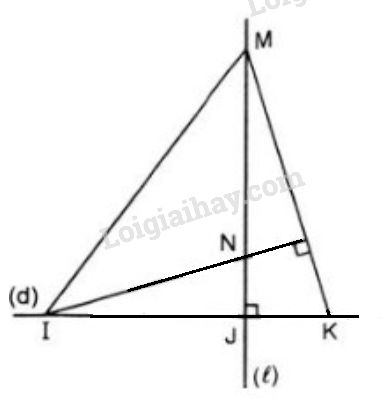
Đề bài

Trên đường thẳng \(d\), lấy ba điểm phân biệt  \(I, J, K\) (\(J\) ở giữa \(I\) và \(K\))

Kẻ đường thẳng \(l\) vuông góc với \(d\) tại \(J\), trên \(l\) lấy điểm \(M\) khác với điểm \(J\). Đường thẳng qua \(I\) vuông góc với \(MK\) cắt \(l\) tại \(N\). Chứng minh rằng \(KN ⊥ IM.\)

Lời giải chi tiết

Nối \(M\) với \(I\) ta được \(ΔMIK.\)

Trong \(ΔMIK\) có: \(MJ ⊥ IK\) (do \(l ⊥ d\)) và \(IN ⊥ MK\) (giả thiết)

Nên \(MJ,IN\) là hai đường cao của \(ΔMIK.\)

Mà \(MJ\) và \(IN\) cắt nhau tại \(N\) nên \(N\) là trực tâm của \(ΔMIK.\)

Suy ra \(KN\) là đường cao thứ ba của \(ΔMIK\) hay \(KN ⊥ IM\) (điều phải chứng minh).

Loigiaihay.com