Bài 50 trang 49 SGK giải tích 12 nâng caoKhảo sát sự biến thiên và vẽ đồ thị hàm số sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
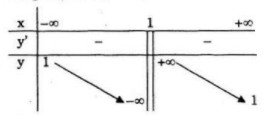
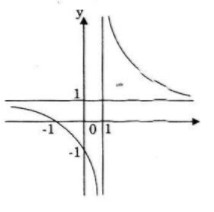
Khảo sát sự biến thiên và vẽ đồ thị hàm số sau: LG a \(y = {{x + 1} \over {x - 1}}\) Lời giải chi tiết: TXĐ: \(D =\mathbb R\backslash \left\{ 1 \right\}\) Vì \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 1\) nên \(y = 1\) là tiệm cận ngang. \(y = {{1.(-1)-1.1} \over {{{\left( {x - 1} \right)}^2}}} = {{ - 2} \over {{{\left( {x - 1} \right)}^2}}} < 0\) với mọi \(x \ne 1\)
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) Hàm số không có cực trị.
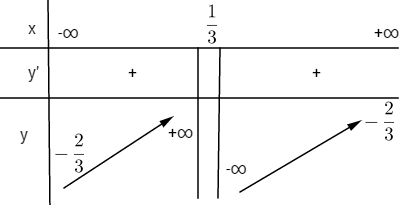
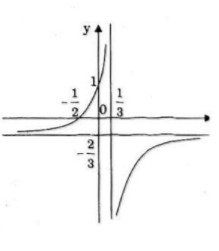
LG b \(y = {{2x + 1} \over {1 - 3x}}\) Lời giải chi tiết: TXĐ: \(D =\mathbb R\backslash \left\{ {{1 \over 3}} \right\}\) Vì \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty }y = - {2 \over 3}\) nên \(y = - {2 \over 3}\) là tiệm cận ngang. \(y = {{2.1-(-3).1} \over {{{\left( {1 - 3x} \right)}^2}}} = {5 \over {{{\left( {1 - 3x} \right)}^2}}} > 0\) với mọi \(x \ne {1 \over 3}\)
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;{1 \over 3}} \right)\) và \(\left( {{1 \over 3}; + \infty } \right)\) Hàm số không có cực trị.
Loigiaihay.com
|




















Danh sách bình luận