Bài 5 trang 56 SGK Toán 7 tập 2Ba bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường .. Quảng cáo
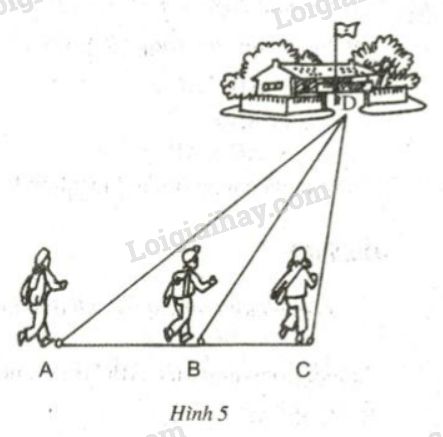
Đề bài Ba bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường \(AD, BD,\) và \(CD\) (hình dưới). Biết rằng ba điểm \(A, B, C \) cùng nằm trên một đường thẳng và góc \(ACD\) là góc tù. Hỏi ai đi xa nhất, ai đi gần nhất? Hãy giải thích
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: - Định lí quan hệ giữa góc và cạnh đối diện - Góc ngoài tam giác bằng tổng hai góc trong không kề với nó. Do đó góc ngoài tam giác lớn hơn các góc trong không kề với nó. Lời giải chi tiết Vì \(\widehat{ACD}\) tù (gt) nên \(∆DCB\) có \(\widehat{C}>\widehat{CBD}\) (góc tù là góc lớn nhất trong tam giác) \( \Rightarrow BD > CD\) (1) (đối diện với góc lớn hơn là cạnh lớn hơn) \(\Delta ABD \) có \(\widehat{DBA}\) là góc ngoài của \( \Delta DCB\) nên \(\widehat{DBA}=\widehat{DCB}+\widehat{BDC}\) \( \Rightarrow \widehat{DBA}\) > \(\widehat{DCB}\) Vì \(\widehat{DCB}\) là góc tù nên \(\widehat{DBA}\) là góc tù Do đó \(\widehat{DBA}\) là góc lớn nhất trong \(\Delta ABD \) nên AD là cạnh lớn nhất trong \(\Delta ABD \) (đối diện với góc lớn nhất là cạnh lớn nhất) \(\Rightarrow AD > BD\) (2) Từ (1) và (2) \( \Rightarrow\) \(AD > BD >CD\) Vậy Hạnh đi xa nhất, Trang đi gần nhất. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
