Bài 49 trang 93 SGK Toán 8 tập 1

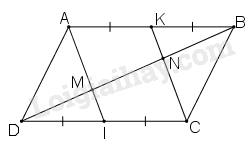
Đề bài

Cho hình bình hành $ABCD.$ Gọi $I, K$ theo thứ tự là trung điểm của $CD, AB.$ Đường chéo $BD$ cắt $AI, CK$ theo thứ tự ở $M$ và $N.$ Chứng minh rằng:

a) $AI // CK$

b) $DM = MN = NB$

Lời giải chi tiết

a) Vì $ABCD$ là hình bình hành (giả thiết) 

$\Rightarrow \left\{ \begin{array}{l} AB = C{\rm{D}}\\ AB//C{\rm{D}} \end{array} \right.$ (tính chất hình bình hành)

Mà $I, K$ theo thứ tự là trung điểm của $CD, AB$ (giả thiết)

$\Rightarrow \left\{ \begin{array}{l} AK =KB= \dfrac{{AB}}{2}\\ IC =ID= \dfrac{{DC}}{2} \end{array} \right.$ (tính chất trung điểm)

Mà $AB=CD$ (chứng minh trên) nên $\dfrac{AB}2=\dfrac{CD}2$

$\Rightarrow AK = IC$

Lại có: $AB//DC\left( \text{chứng minh trên} \right)$ $\Rightarrow AK//IC$ 

Tứ giác $AICK$ có:

$\left\{ \begin{array}{l} AK//IC\\ AK = IC \end{array} \right.\left( \text{chứng minh trên} \right)$

$\Rightarrow$ Tứ giác $AICK$ là hình bình hành (dấu hiệu nhận biết hình bình hành)

$\Rightarrow AI // CK$ (tính chất hình bình hành)

b) $∆DCN$ có $DI = IC$ (chứng minh trên), $IM // CN$ (vì $AI // KC$)

$\Rightarrow  DM = MN$   (1) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)

 Xét $∆ABM$ có $AK = KB$ (chứng minh trên) và $KN // AM$ ( vì $AI // CK$)

$\Rightarrow  MN = NB$.   (2) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)

Từ (1) và (2) $\Rightarrow DM = MN = NB.$

Loigiaihay.com