Bài 4.9 trang 100 SGK Toán 11 tập 1 - Cùng khám phá

Đề bài

Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là một điểm di động trên cạnh SC.

a) Tìm giao điểm N của SD và mặt phẳng (ABM).

b) Gọi I là giao điểm của hai đường thẳng BM và AN. Chứng minh rằng I nằm trên một đường thẳng cố định khi M di động trên cạnh SC.

Lời giải chi tiết

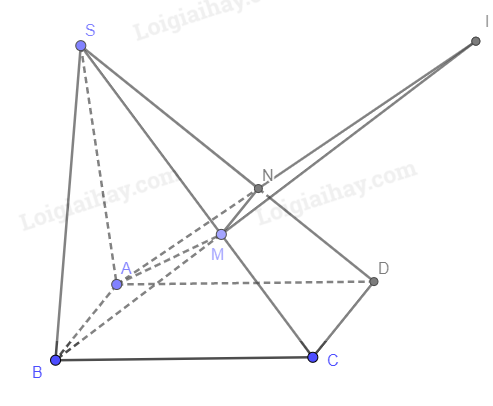
a) Ta có:

\(\left\{ \begin{array}{l}M \in \left( {SCD} \right) \cap \left( {ABM} \right)\\AB \subset \left( {ABM} \right)\\CD \subset \left( {SCD} \right)\\AB//CD\end{array} \right.\)

Suy ra giao tuyến của (SCD) và (ABM) là đường thẳng d đi qua M là song song với AB, BC.

Vậy N là giao điểm của đường thẳng d và SD.

b) (SAD) và (SBC) có chung điểm S và AD//BC. Nên  giao tuyến của (SAD) và (SBC) là đường thẳng đi qua S và song song với AD, BC.

Ta có: \(\left\{ \begin{array}{l}I = BM \cap AN\\BM \subset \left( {SBC} \right)\\AN \subset \left( {SAD} \right)\end{array} \right.\)

Suy ra I nằm trên giao tuyến của (SBC) và (SAD) chính là đường thẳng đi qua S và song song với AD, BC.

Vì S, AD cố định nên I luôn nằm trên đường thẳng cố định đi qua S và song song với AD.