Bài 47 trang 135 SGK Đại số 10 nâng caoGọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
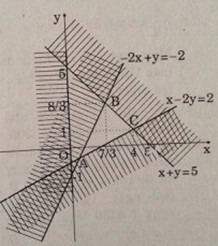
Gọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ: \(\left\{ \matrix{ LG a Hãy xác định (S) để thấy rằng đó là một tam giác. Lời giải chi tiết: Lần lượt dựng các đường thẳng: \((d_1):-2x + y = -2;\) \((d_2): x – 2y = 2; \) \((d_3):x + y = 5\) và \((d_4):x = 0\). Xét điểm M(1;1) ta thấy, M thuộc miền nghiệm của bpt 2, 3, 4 nhưng không thuộc miền nghiệm của 1. Từ đó ta có miền nghiệm của hệ bất phương trình. Tập nghiệm S được biểu diễn bằng miền trong của tam giác ABC với: \(A({2 \over 3};\, - {2 \over 3});\,\,B({7 \over 3};\,{8 \over 3});\,C(4,\,1)\) Ở đó, A là giao điểm của \((d_1)\) và \((d_2)\). B là giao điểm của \((d_1)\) và \((d_3)\). C là giao điểm của \((d_2)\) và \((d_3)\). LG b Trong (S) hãy tìm điểm có tọa độ \((x; y)\) làm cho biểu thức \(f(x;y)=y-x\) có giá trị nhỏ nhất, biết rằng \(f(x;y)\) có giá trị nhỏ nhất tại một trong các đỉnh của (S). Lời giải chi tiết: Tại \(A({2 \over 3};\, - {2 \over 3}) \Rightarrow F = - \frac{2}{3} - \frac{2}{3}= - {4 \over 3}\) Tại \(B({7 \over 3};\,{8 \over 3}) \Rightarrow F =\frac{8}{3} - \frac{7}{3}= {1 \over 3}\) Tại \(C(4; 1)\) thì \(F = 1-4=-3\) Vậy F đạt giá trị nhỏ nhất bằng -3 tại \(C(4, 1)\). Loigiaihay.com
|




















Danh sách bình luận