Bài 44 trang 20 SGK Toán 8 tập 1Phân tích các đa thức sau thành nhân tử: Quảng cáo
Video hướng dẫn giải Phân tích các đa thức sau thành nhân tử: LG a \({x^3} + \dfrac{1}{27}\); Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Tổng hai lập phương. \(6)\,{A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\) Lời giải chi tiết: \(\begin{array}{l} LG b \({\left( {a + b} \right)^3} - {\left( {a - b} \right)^3}\); Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ: Hiệu hai lập phương, bình phương một tổng, bình phương một hiệu, hiệu hai bình phương. \(1)\,{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) \(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) \(3)\,{A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) \(7)\,{A^3} - {B^3} = \left( {A - B} \right)({A^2} + AB + {B^2})\) Lời giải chi tiết:
LG c \({\left( {a + b} \right)^3} + {\left( {a - b} \right)^3}\); Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ: Tổng hai lập phương, bình phương một tổng, bình phương một hiệu, hiệu hai bình phương. \(1)\,{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) \(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) \(3)\,{A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) \(6)\,{A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\) Lời giải chi tiết:
LG d \(8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}\) Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Lập phương một tổng. \(4)\,{\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) Lời giải chi tiết: \(\,\,8{x^3} + 12{{\rm{x}}^2}y + 6{\rm{x}}{y^2} + {y^3}\\ = {\left( {2{\rm{x}}} \right)^3} + 3.{\left( {2{\rm{x}}} \right)^2}.y + 3.2{\rm{x}}.{y^2} + {y^3}\\ = {\left( {2{\rm{x}} + y} \right)^3}\) LG e \( - {x^3} + 9{x^2} - 27x + 27.\) Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: Lập phương một hiệu. \(5)\,{\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) Lời giải chi tiết: \(\begin{array}{l} Loigiaihay.com
|














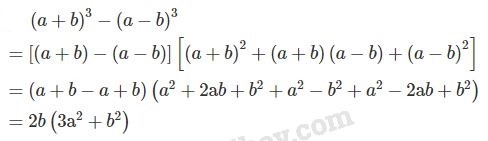
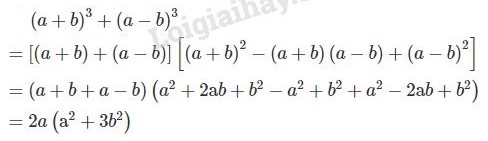






Danh sách bình luận