Bài 43 trang 63 SGK Đại số 10 nâng caoLập bảng biến thiên và vẽ đồ thị của hàm số. Quảng cáo
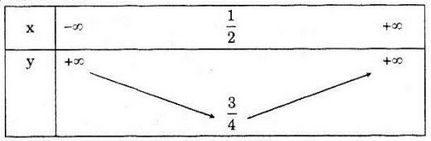
Đề bài Xác định các hệ số a, b và c để cho hàm số \(y = ax^2 + bx + c\) đạt giá trị nhỏ nhất bằng \({3 \over 4}\) khi \(x = {1 \over 2}\) và nhận giá trị bằng 1 khi x = 1. Lập bảng biến thiên và vẽ đồ thị của hàm số. Phương pháp giải - Xem chi tiết - Đặt \(f(x) = ax^2 + bx + c\). - Lập hệ phương trình ẩn a, b, c. - Giải hệ suy ra hàm số cần tìm và lập bảng biến thiên. Chú ý: Hàm số \(f(x) = ax^2 + bx + c\,\,(a>0)\) đạt GTNN tại \(x = - \frac{b}{{2a}}\) Lời giải chi tiết Đặt \(f(x) = ax^2 + bx + c\). +) Hàm số \(f(x) = ax^2 + bx + c\) đạt GTNN tại \(x = - \frac{b}{{2a}}\) nên \( - \frac{b}{{2a}} = \frac{1}{2}\,\,\,(1)\) +) GTNN đạt được bằng \({3 \over 4}\) khi \(x = {1 \over 2}\) nên \(f\left( {\frac{1}{2}} \right) = \frac{3}{4}\) \( \Leftrightarrow a.{\left( {\frac{1}{2}} \right)^2} + b.\frac{1}{2} + c = \frac{3}{4}\)\( \Leftrightarrow \frac{1}{4}a + \frac{1}{2}b + c = \frac{3}{4}\,\,\left( 2 \right)\) +) \(f\left( 1 \right) = 1 \)\(\Leftrightarrow a{.1^2} + b.1 + c = 1\)\( \Leftrightarrow a + b + c = 1\,\,\left( 3 \right)\) Từ (1) (2) và (3) ta có hệ: \(\left\{ \matrix{ \(\Leftrightarrow \left\{ \matrix{ Vậy \(y = x^2 – x + 1\) Bảng biến thiên:
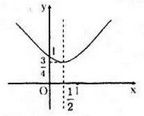
Đồ thị hàm số:
Loigiaihay.com
|




















Danh sách bình luận