Bài 41 trang 63 SGK Đại số 10 nâng cao

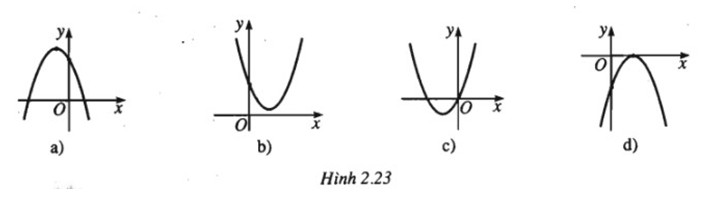
Đề bài

Dựa vào đồ thị của hàm số \(y = ax^2 + bx + c\). Hãy xác định dấu của các hệ số a, b và c trong mỗi trường hợp dưới đây:

Lời giải chi tiết

a) Parabol (P₁) có bề lõm quay xuống nên a < 0

(P₁) cắt trục Oy tại điểm có tung độ dương nên c = f(0) > 0

Hoành độ đỉnh \({x_0} =  - {b \over {2a}} < 0 \)

\( \Leftrightarrow \frac{b}{{2a}} > 0\) (b và a cùng dấu)

\(\Rightarrow b < 0\)  (do a <0)

b) Parabol (P₂) có bề lõm quay lên nên a > 0

(P₁) cắt trục Oy tại điểm có tung độ dương nên c = f(0) > 0

Hoành độ đỉnh \({x_0} =  - {b \over {2a}}\) > 0

\( \Leftrightarrow \frac{b}{{2a}} < 0\) (b và a trái dấu)

⇒ b < 0  (do a >0)

c) Parabol (P₃) có bề lõm quay lên nên a > 0

(P₃) đi qua gốc O nên c = 0

Hoành độ đỉnh \({x_0} =  - {b \over {2a}}\) < 0

\( \Leftrightarrow \frac{b}{{2a}} > 0\) (b và a cùng dấu)

⇒ b > 0  (do a >0)

d) Parabol (P₃) có bề lõm quay xuống nên a < 0

(P₃) cắt trục Oy tại điểm có tung độ âm nên c < 0

Hoành độ đỉnh \({x_0} =  - {b \over {2a}}\) > 0

\( \Leftrightarrow \frac{b}{{2a}} < 0\) (b và a trái dấu)

⇒ b > 0  (do a < 0)

Loigiaihay.com