Bài 4.26 trang 94 SGK Toán 11 tập 1 - Kết nối tri thứcCho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của hai tam giác ABC và A’B’C’. a) Chứng minh rằng tứ giác AGG’A’ là hình bình hành b) Chứng minh rằng AGC.A’G’C’ là hình lăng trụ Quảng cáo
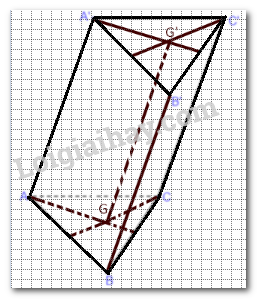
Đề bài Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của hai tam giác ABC và A’B’C’. a) Chứng minh rằng tứ giác AGG’A’ là hình bình hành. b) Chứng minh rằng AGC.A’G’C’ là hình lăng trụ. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Sử dụng định nghĩa hình bình hành và hình lăng trụ để chứng minh. Lời giải chi tiết
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'. Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'. Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành. b) AGG'A' là hình bình hành suy ta AA' // GG'. Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ). Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
