Bài 4 trang 79 Tài liệu dạy – học Toán 9 tập 2

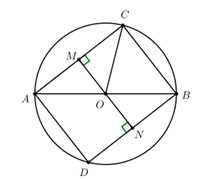
Đề bài

Cho đường tròn (O) đường kính AB. Qua A và B vẽ hai dây song song AC và BD (điểm C và D nằm trên đường tròn). Gọi M, N lần lượt là hình chiếu vuông góc của O xuống AC và BD.

a) So sánh OM và ON.

b) So sánh hai cung AC và BD.

Lời giải chi tiết

 

a) Xét tam giác vuông OAM và tam giác vuông OBN có:

\(OA = OB = R\)

\(\widehat {AOM} = \widehat {BON}\) (đối đỉnh)

\( \Rightarrow {\Delta _v}AOM = {\Delta _v}BON\,\,\) (cạnh huyền – góc nhọn)

\( \Rightarrow OM = ON\).

b) Vì \(OM = OB \Rightarrow AC = BD\) (Hai dây cách đều tâm thì bằng nhau) => cung AC = cung BD (Hai dây bằng nhau căng hai cung bằng nhau).

 Loigiaihay.com