Bài 38 trang 73 SGK Toán 7 tập 2

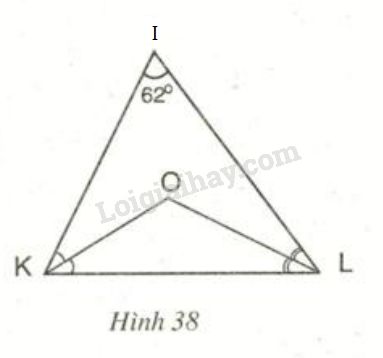
Đề bài

Cho hình 38.

 

a)   Tính góc \(KOL\).

b)   Kẻ tia \(IO\), hãy tính góc \(KIO\).

c)   Điểm \(O\) có cách đều ba cạnh của tam giác \(IKL\) không? Tại sao?

Lời giải chi tiết

a) \(∆KIL\) có \(\widehat{I} + \widehat{IKL}+ \widehat{ILK} =180^o\) (Theo định lí tổng ba góc trong một tam giác) 

Mà \(\widehat{I} =62^o\)  nên \(\widehat{IKL}+ \widehat{ILK} = 180^o - 62^o = 118^o \) 

Vì \(KO\) và \(LO\) lần lượt là phân giác  \(\widehat{IKL}\), \(\widehat{ILK}\) nên \(\widehat {OKL} = \dfrac{1}{2}\widehat {IKL},\,\,\widehat {OLK} = \dfrac{1}{2}\widehat {ILK}\)

Suy ra \(\widehat{OKL}+ \widehat{OLK}= \dfrac{1}{2}(\widehat{IKL}+ \widehat{ILK})\)

\(\Rightarrow\) \(\widehat{OKL}+ \widehat{OLK} = \dfrac{1}{2}. 118^o\)

\(\Rightarrow\) \(\widehat{OKL}+ \widehat{OLK} = 59^o\) 

\(∆KOL\) có \(\widehat{OKL}+ \widehat{OLK} + \widehat{KOL} =180^o \) (Theo định lí tổng ba góc trong một tam giác)

Mà \(\widehat{OKL}+ \widehat{OLK} = 59^o\)  nên \(\widehat{KOL} = 180^o -59^o = 121^o\) 

b) \(ΔKIL\) có \(O\) là giao điểm của hai đường phân giác \(KO\) và \(LO\) nên \(IO\) là đường phân giác của góc \(KIL\) (định lí ba đường phân giác cùng đi qua một điểm).

Do đó: \( \widehat{KIO} = \dfrac{\widehat{KIL}}{2}= \dfrac{62^0}{2} = 31^o\)

c) Vì \(O\) là giao điểm của ba đường phân giác của tam giác \(IKL\) nên \(O\) cách đều ba cạnh của tam giác \(IKL\). (Theo định lí về tính chất của ba đường phân giác trong tam giác)

Loigiaihay.com