Bài 42 trang 73 SGK Toán 7 tập 2

Đề bài

Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.

Gợi ý : Trong \(∆ABC\), nếu \(AD\) vừa là đường trung tuyến vừa là đường phân giác thì kéo dài \(AD\) một đoạn \(D{A_1}\) sao cho \(D{A_1}= AD.\)

Lời giải chi tiết

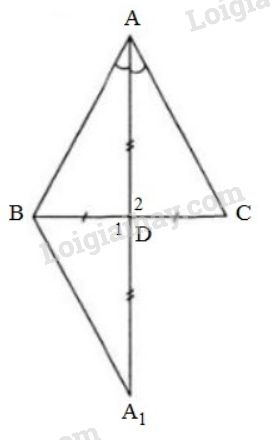
Gọi \(AD\) là đường trung tuyến đồng thời là đường phân giác của góc \(A\) trong \(ΔABC.\)  Ta chứng minh  \(∆ABC\) cân tại \(A.\)

Kéo dài \(AD\) một đoạn \(D{A_1}= AD.\)

Xét \(∆ADC\) và \(∆{A_1}DB\) ta có:

+) \(DC = DB\) (do \(AD\) là trung tuyến)

+) \({ \widehat{D}}_1 = {\widehat{D}}_2 \) (\(2\) góc đối đỉnh)

 +) \(AD = D{A_1}\) (do cách vẽ)

Vậy \(∆ADC =  ∆{A_1}DB\) (c.g.c)

\(\Rightarrow AC = {A_1}B\)( 2 cạnh tương ứng)(1); \(\widehat{DAC}= \widehat{DA_1B}\) ( 2 góc tương ứng)

Mà \(\widehat{BAD}= \widehat{DAC}\) (Vì \(AD\) là phân giác của \(\widehat{BAC}\))

\(\Rightarrow \) \(\widehat{BAD}=\widehat{DA_1B}\)

\(\Rightarrow \) Tam giác \(AB{A_1}\) cân tại \(B\) 

\(\Rightarrow AB = {A_1}B\)           (2)

Từ (1) và (2) \(\Rightarrow \) \(AB = AC\).

Vậy \(∆ABC\) cân tại \(A.\)

Vậy: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân (đpcm)