Bài 38 trang 61 SGK Đại số 10 nâng caoTìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
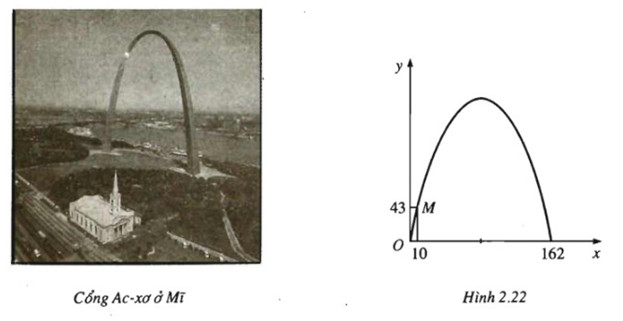
(Bài toán về cổng Ac-xơ (Arch)) Khi du lịch đến thành phố Xanh lu-i (Mĩ) bạn sẽ thấy một cái cổng lớn hình parabol hướng bề lõm về phía dưới. Đó là cổng Ac-xơ. Giả sử lập một hệ tọa độ Oxy sao cho một chân cổng đi qua gốc O như hình vẽ dưới đây (x, y tính bằng mét), chân kia của cổng ở vị trí (162; 0). Biết một điểm M trên cổng có tọa độ là (10; 43).
LG a Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn). Lời giải chi tiết: Giả sử hàm số bậc hai có đồ thị chứa cung parabol trên là: \(f(x) = ax^2 + bx + c\) Theo đề bài, ta có: \(\left\{ \matrix{ \(\Leftrightarrow \left\{ \matrix{ Vậy: \(f(x) = - {{43} \over {1520}}{x^2} + {{3483} \over {760}}x\) LG b Tính chiều cao của cổng (Tính từ điểm cao nhất trên cổng xuống mặt đất, tính chính xác đến hàng đơn vị). Phương pháp giải: Chiều cao của cổng là GTLN của hàm số. Lời giải chi tiết: Chiều cao của cổng bằng tung độ của đỉnh parabol Ta có: \(\begin{array}{l} Vậy chiều cao cổng là 186m. Loigiaihay.com
|




















Danh sách bình luận