Bài 34 trang 60 SGK Đại số 10 nâng cao

LG a

(P) nằm hoàn toàn ở phía trên trục hoành

Phương pháp giải:

Nhận xét dựa vào bề lõm và đỉnh của parabol.

Lời giải chi tiết:

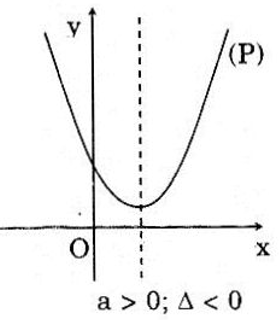
(P) nằm hoàn toàn phía trên trục hoành thì bề lõm hướng lên và đỉnh \(I( - {b \over {2a}};-{\Delta  \over {4a}})\) nằm phía trên trục hoành nên 

\(\left\{ \begin{array}{l}
a > 0\\
- \frac{\Delta }{{4a}} > 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a > 0\\
\Delta < 0
\end{array} \right.\)

Cách khác:

(P) nằm hoàn toàn phía trên trục hoành thì:

+) Bề lõm hướng lên nên \(a > 0\)

+) (P) nằm hoàn toàn phía trên trục hoành nghĩa là \(\left( P \right) \cap Ox = \emptyset \) hay phương trình \(a{x^2} + bx + c = 0\) vô nghiệm \( \Leftrightarrow \Delta  < 0\)

Vậy \(a > 0,\Delta  < 0\)

LG b

(P) nằm hoàn toàn ở phía dưới trục hoành

Lời giải chi tiết:

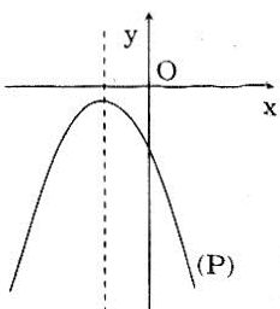
(P) nằm hoàn toàn phía dưới trục hoành thì:

+) bề lõm hướng xuống nên \(a < 0\).

+) đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) nằm phía dưới trục hoành nên \( - \frac{\Delta }{{4a}} < 0 \Leftrightarrow \frac{\Delta }{{4a}} > 0 \Leftrightarrow \Delta  < 0\)

(vì \(a < 0\))

Vậy (P) nằm hoàn toàn phía dưới trục hoành thì a < 0 và Δ < 0.

LG c

(P) cắt trục hoành tại hai điểm phân biệt và đỉnh của (P) nằm phía trên trục hoành

Lời giải chi tiết:

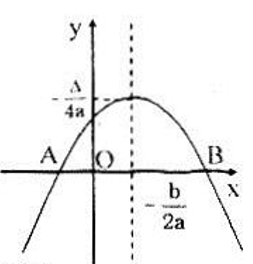
(P) phải có hình dạng ở hình vẽ trên, do đó phương trình ax² + bx + c = 0 có hai nghiệm phân biệt ⇔ Δ > 0

Đỉnh của (P) nằm phía trên trục hoành nên

\( - \frac{\Delta }{{4a}} > 0 \Leftrightarrow \frac{\Delta }{{4a}} < 0\)

Do đó \(\Delta\) và a trái dấu nên a < 0 (do Δ > 0)

Vậy (P) cắt trục hoành tại hai điểm phân biệt và đỉnh của (P) nằm phía trên trục hoành thì a < 0 và Δ > 0.

Loigiaihay.com