Bài 35 trang 79 SGK Toán 8 tập 2

Đề bài

Chứng minh rằng nếu tam giác $A'B'C'$ đồng dạng với tam giác $ABC$ theo tỉ số $k$ thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng $k$.

Lời giải chi tiết

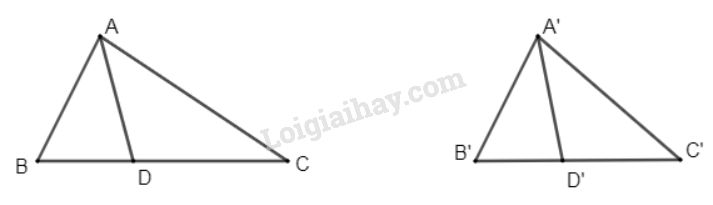
Gọi $AD, A'D'$ lần lượt là đường phân giác của hai tam giác $ABC;\,A'B'C'$

Ta có: $∆A'B'C' ∽ ∆ABC$ theo tỉ số $k= \dfrac{A'B'}{AB}$ 

$\Rightarrow \widehat {BAC} = \widehat {B'A'C'}$   (1); $\widehat{B}$ = $\widehat{B'}$ (tính chất hai tam giác đồng dạng)

$AD$ là phân giác góc $\widehat {BAC}$ (gt)

$\Rightarrow$ $\widehat {BAD} = \dfrac{1}{2}\widehat {BAC}$     (2) (tính chất tia phân giác)

$A'D'$ là phân giác góc $\widehat {B'A'C'}$ (gt)

$\Rightarrow$  $\widehat {B'A'D'} =\dfrac{1}{2}\widehat {B'A'C'}$   (3) (tính chất tia phân giác)

Từ $(1),(2)$ và $(3)$ suy ra: $\widehat{BAD}$ = $\widehat{B'A'D'}$

Xét $∆A'B'D'$ và $∆ABD$ có:

+) $\widehat{B}$ = $\widehat{B'}$

+) $\widehat{BAD}$ = $\widehat{B'A'D'}$ (chứng minh trên)

$\Rightarrow ∆A'B'D' ∽ ∆ABD$ (g-g) 

$\Rightarrow \dfrac{A'D'}{AD}=\dfrac{A'B'}{AB}=k$ ( cặp cạnh tương ứng tỉ lệ)