Bài 31 trang 48 SGK Toán 8 tập 2

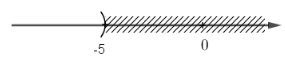
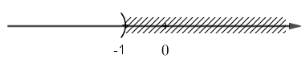
LG a.

$\dfrac{{15 - 6x}}{3} > 5$  

Phương pháp giải:

 Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.

Lời giải chi tiết:

Ta có

$\eqalign{ & {{15 - 6x} \over 3} > 5 \cr  & \Leftrightarrow 15 - 6x > 5.3 \cr  & \Leftrightarrow 15 - 6x > 15  \cr  & \Leftrightarrow - 6x > 0 \cr  & \Leftrightarrow x < 0 \cr}$ 

Vậy bất phương trình có tập nghiệm là S = {$x|x < 0$} và được biểu diễn trên trục số như sau:

LG b.

$\dfrac{{8 - 11x}}{4} < 13$

Phương pháp giải:

 Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.

Lời giải chi tiết:

Ta có                                        

$\begin{array}{l}\dfrac{{8 - 11x}}{4} < 13\\ \Leftrightarrow 8 - 11x < 13.4\\ \Leftrightarrow 8 - 11x < 52\\ \Leftrightarrow  - 11x < 44\\ \Leftrightarrow x >  - 4\end{array}$ 

Vậy bất phương trình có tập nghiệm là S ={ $x|x >  - 4$} và được biểu diễn trên trục số như sau: 

LG c.

$\dfrac{1}{4}\left( {x - 1} \right) < \dfrac{{x - 4}}{6}$  

Phương pháp giải:

 Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.

Lời giải chi tiết:

Ta có

$\eqalign{ & {1 \over 4}\left( {x - 1} \right) < {{x - 4} \over 6} \cr  & \Leftrightarrow 12.{1 \over 4}\left( {x - 1} \right) < 12.{{x - 4} \over 6} \cr  & \Leftrightarrow 3x - 3 < 2x - 8  \cr  & \Leftrightarrow x < - 5 \cr}$

Vậy bất phương trình có tập nghiệm là S ={ $x| x <  - 5$} và được biểu diễn trên trục số như sau: 

LG d.

$\dfrac{{2 - x}}{3} < \dfrac{{3 - 2x}}{5}$

Phương pháp giải:

 Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.

Lời giải chi tiết:

Ta có

$\begin{array}{l}\dfrac{{2 - x}}{3} < \dfrac{{3 - 2x}}{5}\\ \Leftrightarrow \dfrac{{10 - 5x}}{{15}} < \dfrac{{9 - 6x}}{{15}}\\ \Leftrightarrow 10 - 5x < 9 - 6x\\ \Leftrightarrow - 5x + 6x < 9 -10\\ \Leftrightarrow x <  - 1\end{array}$

Vậy bất phương trình có tập nghiệm là S = {$x|x <  - 1$} và được biểu diễn trên trục số như sau: