Bài 30 trang 66 SGK Hình học 10 nâng caoCho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC và BD. Quảng cáo
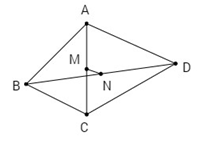
Đề bài Cho tứ giác \(ABCD\). Gọi \(M, N\) lần lượt là trung điểm của \(AC\) và \(BD\). Chứng minh rằng: \(A{B^2} + B{C^2} + C{D^2} + D{A^2}\)\( = A{C^2} + B{D^2} + 4M{N^2}\). Phương pháp giải - Xem chi tiết - Áp dụng công thức trung tuyến trong các tam giác: + BMD để tính MN. + BAC để tính BM. + DAC để tính DM. - Từ đó biến đổi suy ra đpcm. Lời giải chi tiết Áp dụng công thức tính trung tuyến, \(MN\) là trung tuyến của tam giác \(BMD\), ta có \(M{N^2} = {{B{M^2} + D{M^2}} \over 2} - {{B{D^2}} \over 4}\) \(\Leftrightarrow \,\,4M{N^2} = 2(B{M^2} + D{M^2}) - B{D^2}\) Mà \(BM, DM\) lần lượt là trung tuyến của tam giác \(ABC, ADC\) nên Cách khác: * Áp dụng công thức trung tuyến của tam giác ta có: \(\begin{array}{l}m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4}\\ \Leftrightarrow \frac{{{b^2} + {c^2}}}{2} = m_a^2 + \frac{{{a^2}}}{4}\\ \Leftrightarrow {b^2} + {c^2} = 2m_a^2 + \frac{{{a^2}}}{2}\,\,\,\left( * \right)\end{array}\) * Áp dụng công thức (*) Trong tam giác ABD ta có : AB2 + AD2 = 2AN2 + BD2/2 (1) Trong tam giác CBD ta có : CD2 + CB2 = 2CN2 + BD2/2 (2) Cộng vế với vế của (1) và (2) ta có : AB2 + BC2 + CD2 + DA2 = 2(AN2 + CN2) + BD2(3) Xét tam giác CAN ta có : AN2 + CN2 = 2MN2 + AC2/2 (4) (vì M là trung điểm AC) Thay (4) vào (3) ta được : AB2 + BC2 + CD2 + DA2 = 2[2MN2 + AC2/2] + BD2 = AC2 + BD2 + 4MN2 Loigiaihay.com
|














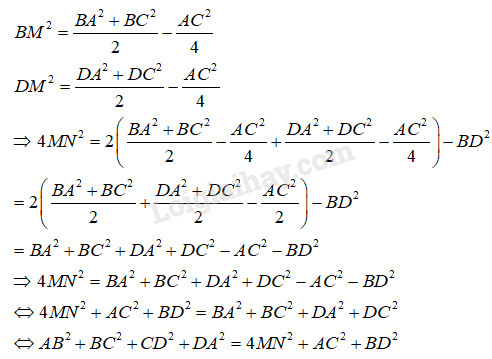






Danh sách bình luận