Bài 30 trang 59 SGK Toán 9 tập 1

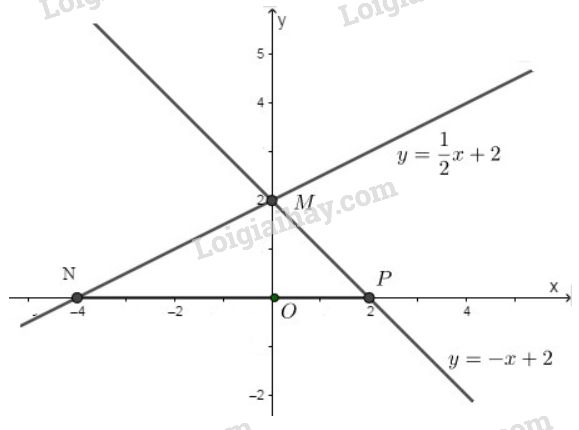
Đề bài

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau: 

$y = \dfrac{1}{2}x + 2$;                                      $y = -x + 2$

b) Gọi giao điểm của hai đường thẳng $y = \dfrac{1}{2}x + 2$  và  $y = -x + 2$ với trục hoành theo thứ tự là $A, B$ và gọi giao điểm của hai đường thẳng đó là $C$. Tính các góc của tam giác $ABC$ (làm tròn đến độ).

c) Tính chu vi và diện tích của tam giác $ABC$ (đơn vị đo trên các trục tọa độ là xentimét)

Lời giải chi tiết

a) Đồ thị được vẽ như hình dưới:

+) Hàm số $y = \dfrac{1}{2}x + 2$:     

     Cho $x=0 \Rightarrow y=\dfrac{1}{2}.0 + 2=0+2=2 \Rightarrow M(0; 2)$.

     Cho $y=0 \Rightarrow 0=\dfrac{1}{2}.x + 2 \Rightarrow x=-4 \Rightarrow N(-4; 0)$.

Đồ thị hàm số $y = \dfrac{1}{2}x + 2$ là đường thẳng đi qua hai điểm $M(0; 2)$ và $N(-4; 0)$

+) Hàm số  $y = -x + 2$:

     Cho $x=0 \Rightarrow y=0 + 2=2 \Rightarrow M(0; 2)$.

     Cho $y=0 \Rightarrow 0=-x + 2 \Rightarrow x= 2 \Rightarrow P(2; 0)$.

Đồ thị hàm số $y = -x + 2$   là đường thẳng đi qua hai điểm $M(0; 2)$ và $P(2; 0)$ 

      

b) +) Hoành độ điểm $C$ là nghiệm của phương trình:

$\dfrac{1}{2}x+2=-x+2$

$\Leftrightarrow \dfrac{1}{2}x+x=2-2$

$\Leftrightarrow \dfrac{3}{2}x=0$

$\Leftrightarrow x=0$

Do đó tung độ của $C$ là: $y=0+2=2$. Vậy $C(0; 2) \equiv M$.

 +) Vì $A$ thuộc trục hoành $Ox$ nên tung độ của $A$ bằng $0$. Thay $y=0$ vào $y=\dfrac{1}{2}x+2$, ta được:

$0=\dfrac{1}{2}x+2$

$\Leftrightarrow \dfrac{1}{2}x=-2$

$\Leftrightarrow x=-4$ 

Vậy $A(-4; 0) \equiv N$.

+) Vì $B$ thuộc trục hoành $Ox$ nên tung độ của $B$ bằng $0$. Thay $y=0$ vào $y=-x+2$, ta được:

$0=-x+2$

$\Leftrightarrow x=2$

Vậy $B(2; 0) \equiv P$.

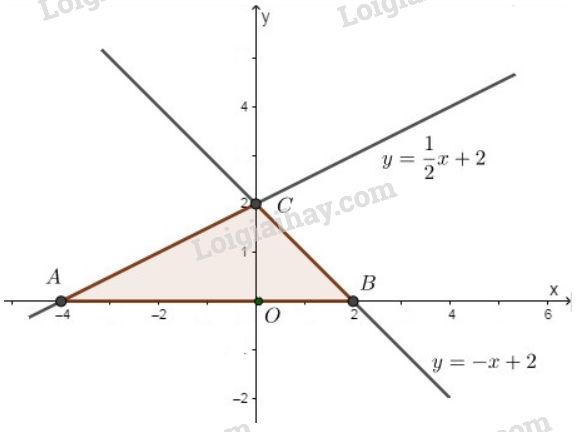
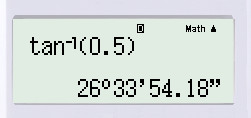
Ta có được $OA=4,\ OB=2,\ OC=2,$$AB=OA+OB=4+2=6$.

Ta có: $OB=OC$ nên tam giác $COB$ vuông cân tại $O$ ($O$ là gốc tọa độ) nên: $\widehat{B}=45^o$

Dùng định nghĩa tỉ số lượng giác đối với tam giác $AOC$ vuông tại $O$, ta có:

                         $\tan A=\dfrac{OC}{OA}=\dfrac{2}{4}=\dfrac{1}{2}$

Thực hiện bấm máy tính, ta được:  $\widehat{A} \approx 27^o$

 

Xét $\Delta{ABC}$ có: $\widehat{A}+ \widehat{B}+\widehat{C}=180^o$

                         $\Leftrightarrow \widehat{C}=180^o-\widehat{A}-\widehat{B}$

                         $\Leftrightarrow  \widehat{C} \approx 180^o-27^o-45^o$

                         $\Leftrightarrow  \widehat{C} \approx 108^o$

c) Ta có: $AB = 6 (cm)$

Xét tam giác vuông $OAC$ vuông tại $O$, theo định lí Py-ta-go, ta có:

                 $AC^2=AO^2+OC^2=4^2+2^2=16+4=20$

             $\Rightarrow AC =\sqrt{20}=2\sqrt{5}(cm)$

Xét tam giác vuông $OBC$ vuông tại $O$, ta có:

                  $BC^2=BO^2+OC^2=2^2+2^2=4+4=8$

              $\Rightarrow BC =\sqrt 8 = 2\sqrt{2}(cm)$

$\Delta{OAC}$ có $CO \bot AB$ nên $CO$ là đường cao ứng với cạnh $AB$.

Chu vi tam giác là:

       $P=AB+BC+AC=6+2\sqrt{5}+2\sqrt{2} (cm)$

Diện tích tam giác là:

       $S=\dfrac{1}{2}.OC.AB=\dfrac{1}{2}.2.6=6 (cm^2)$ 

Loigiaihay.com