Bài 3 trang 56 SGK Toán 7 tập 2Cho tam giác ABC Quảng cáo
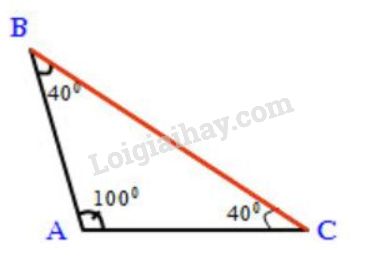
Đề bài Cho tam giác \(ABC\) với \(\widehat{A} = 100^o\) , \(\widehat{B} = 40^o\) a) Tìm cạnh lớn nhất của tam giác. b) Tam giác \(ABC\) là tam giác gì? Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: - Định lí tổng ba góc trong tam giác bằng \(180^0\). - Định lí về mối quan hệ giữa góc và cạnh đối diện. Lời giải chi tiết a) Tam giác \(ABC\) có \(\widehat{A} = 100^o\) và \(\widehat{B} = 40^o\) Áp dụng định lí tổng ba góc trong tam giác vào tam giác \(ABC\) ta được: \(\eqalign{ \( \Rightarrow \widehat A > \widehat B = \widehat C\) \(\left( {{{100}^o} > {{40}^o}} \right)\) Vậy \(\widehat A\) lớn nhất do đó cạnh đối diện với góc A là cạnh \(BC\) lớn nhất (Theo định lí về quan hệ giữa góc và cạnh đối diện)
b) Tam giác \(ABC\) có \(\widehat C = \widehat B = {40^0}\) do đó \(\Delta ABC \) là tam giác cân tại \(A\) Loigiaihay.com
|














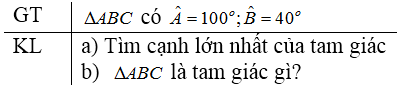






Danh sách bình luận