Bài 3 trang 118 SGK Hình học 10 nâng cao

LG a

Với điều kiện nào của x và y thì điểm M(x, y) thuộc nửa mặt phẳng có bờ d và chứa gốc tọa độ O? Chứng minh điểm A nằm trong nửa mặt phẳng đó.

Lời giải chi tiết:

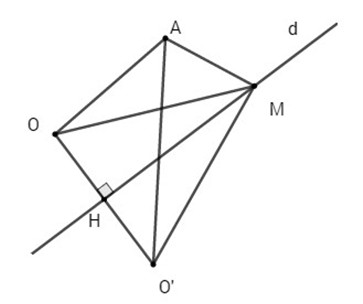
Điểm M(x;y) và O(0;0) nằm cùng phía đối với d khi và chỉ khi

\((x - y + 2).(0 - 0 + 2) > 0\) \( \Leftrightarrow x - y + 2 > 0\)

Xét A(2;0) và O(0;0) ta có: \(({x_A} - {y_A} + 2)(0 - 0 + 2)\)\( = (2 - 0 + 2).2 = 8 > 0\),

Do đó A và O nằm cùng phía so với d hay A nằm trong nửa mặt phẳng có bờ là d và chứa O.

LG b

Tìm điểm đối xứng với điểm O qua đường thẳng d.

Lời giải chi tiết:

Ta có: \(\overrightarrow {{n_d}}  = \left( {1; - 1} \right) \Rightarrow \overrightarrow {{u_d}}  = \left( {1;1} \right)\)

Gọi d’ là đường thẳng qua O và vuông góc với d.

d' qua O(0;0) và nhận \(\overrightarrow {{u_d}}  = \left( {1;1} \right)\) làm VTPT nên phương trình tổng quát của d’ là \(d’: x+y=0\).

Gọi H là hình chiếu của O lên d thì tọa độ H là nghiệm của hệ:

\(\left\{ \matrix{
x - y = - 2 \hfill \cr 
x + y = 0 \hfill \cr} \right.\) \( \Leftrightarrow \left\{ \matrix{
x = - 1 \hfill \cr 
y = 1 \hfill \cr} \right.\)

Vậy \(H(-1, 1)\)

Gọi O’ là điểm đối xứng của O qua d thì H là trung điểm của OO’ do đó

\(\left\{ \matrix{
{x_H} = {{{x_O} + {x_{O'}}} \over 2} \hfill \cr 
{y_H} = {{{y_O} + {y_{O'}}} \over 2} \hfill \cr} \right.\) \( \Leftrightarrow \left\{ \matrix{
{x_{O'}} = 2{x_H} - {x_O} = - 2 \hfill \cr 
{y_{O'}} = 2{y_H} - {y_O} = 2 \hfill \cr} \right.\) 

Vậy \(O'(-2, 2)\)

LG c

Tìm điểm M trên d sao cho chu vi tam giác OMA nhỏ nhất.

Lời giải chi tiết:

OA không đổi nên chu vi tam giác AMO nhỏ nhất  khi tổng MO+MA nhỏ nhất.

Ta có: \(MO = MO'\) \(\Rightarrow MO + MA = MO' + MA \ge AO'\)

\( \Rightarrow \,\,MO + MA\) nhỏ nhất khi A, M, O’ thẳng hàng , khi đó M là giao điểm của d với đường thẳng O’A.

Phương trình O’A :

\(\eqalign{
& {{x - {x_A}} \over {{x_{O'}} - {x_A}}} = {{y - {y_A}} \over {{y_{O'}} - {y_A}}} \cr 
& {{x - 2} \over { - 2 - 2}} = {{y - 0} \over {2 - 0}} \cr &\Leftrightarrow x + 2y - 2 = 0 \cr} \)

Tọa độ M là nghiệm của hệ: 

\(\left\{ \matrix{
x - y = - 2 \hfill \cr 
x + 2y = 2 \hfill \cr} \right.\) \( \Leftrightarrow \left\{ \matrix{
x = - {2 \over 3} \hfill \cr 
y = {4 \over 3} \hfill \cr} \right.\)

Vậy \(M\left( { - {2 \over 3}\,;\,{4 \over 3}} \right)\)

Loigiaihay.com