Bài 28 trang 96 Tài liệu dạy – học Toán 9 tập 2

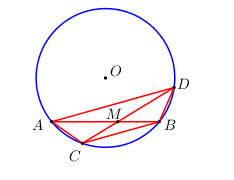
Đề bài

Cho đường tròn (O) và hai dây cung AB, CD bằng nhau và cắt tại điểm M khác O nằm bên trong đường tròn (C nằm trên cung nhỏ AB và B nằm trên cung nhỏ CD).

a) Chứng minh cung AC=BD .

b) Chứng minh hai tam giác MAC và MDB bằng nhau.

c) Tứ giác ACBD là hình gì?

Lời giải chi tiết

 

a) Ta có \(AB = CD \Rightarrow cung\,AB = cung\,CD\)  (hai dây bằng nhau căng hai cung bằng nhau)

\( \Rightarrow cung\,AB - cung\,BC = cung\,CD - cung\,BC \) \(\Leftrightarrow cung\,AC = cung\,BD\).

b) Xét \(\Delta MAC\) và \(\Delta MDB\) có :

\(cung\,AC = cung\,BD \Rightarrow AC = BD\) (hai dây bằng nhau căng hai cung bằng nhau)

\(\widehat {MAC} = \widehat {MDB}\) (hai góc nội tiếp cùng chắn cung BC)

\(\widehat {MCA} = \widehat {MBD}\) (hai góc nội tiếp cùng chắn cung AD)

\( \Rightarrow \Delta MAC = \Delta MDB\,\,\left( {g.c.g} \right)\)

c) Ta có \(cung\,AC = cung\,BD \Rightarrow \widehat {ABC} = \widehat {BAD}\)  (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).

Mà hai góc này ở vị trí so le trong \( \Rightarrow AD//BC \Rightarrow ACBD\) là hình thang.

\(cung\,AB = cung\,CD \Rightarrow \widehat {ADB} = \widehat {CAD}\) (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).

Do đó ACBD là hình thang cân.

 Loigiaihay.com