Bài 27 trang 24 SGK Đại số và Giải tích 12 Nâng cao

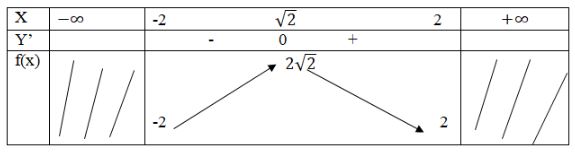
LG a

\(f\left( x \right) = \sqrt {3 - 2x} \) trên đoạn \(\left[ { - 3;1} \right]\);

Lời giải chi tiết:

\(f'\left( x \right) = {{ - 1} \over {\sqrt {3 - 2x\,} }} < 0\) với mọi \(x < {3 \over 2}\,\)

Hàm số \(f\) nghịch biến trên đoạn \(\left[ { - 3;1} \right]\)

Do đó \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 3;1} \right]}  = f\left( { - 3} \right) = 3\); \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 3;1} \right]}  = f\left( 1 \right) = 1\)

Cách khác:

\(f'\left( x \right) = {{ - 1} \over {\sqrt {3 - 2x\,} }} = 0\) vô nghiệm trên đoạn [-3;1] 

Mà \(f\left( { - 3} \right) = 3\); \(f\left( 1 \right) = 1\).

Do đó \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 3;1} \right]}  = f\left( { - 3} \right) = 3\); \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 3;1} \right]}  = f\left( 1 \right) = 1\)

LG b

\(f\left( x \right) = x + \sqrt {4 - {x^2}} \)

Lời giải chi tiết:

TXĐ: \(D = \left[ { - 2;2} \right]\)

\(f'\left( x \right) = 1 - {x \over {\sqrt {4 - {x^2}}}}\) với \(x \in \left( { - 2;2} \right)\)

\(f'\left( x \right) = 0 \Leftrightarrow 1 - {x \over {\sqrt {4 - {x^2}}} } = 0 \) \(\Leftrightarrow \sqrt {4 - {x^2}} = x \Leftrightarrow \left\{ \matrix{
0 < x < 2 \hfill \cr 
4 - {x^2} = {x^2} \hfill \cr} \right. \) \(\Leftrightarrow x = \sqrt 2 \)

Ta có \(f\left( { - 2} \right) =  - 2;f\left( {\sqrt 2 } \right) = 2\sqrt 2 ;\) \(f\left( 2 \right) = 2\)

Vậy \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 2;2} \right]}  = 2\sqrt 2 ;\) \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 2;2} \right]}  =  - 2\)

Cách khác:

BBT:

Vậy \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 2;2} \right]}  = 2\sqrt 2 ;\) \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 2;2} \right]}  =  - 2\)

LG c

\(f\left( x \right) = {\sin ^4}x + {\cos ^2}x + 2;\) 

Lời giải chi tiết:

TXĐ: \(D =\mathbb R\)

Ta có: \(f\left( x \right) = {\sin ^4}x + 1 - {\sin ^2}x + 2 \) \(= {\sin ^4}x - {\sin ^2}x + 3\)

Đặt \(t = {\sin ^2}x;0 \le t \le 1\)

Tìm giá trị nhỏ nhất, lớn nhất của hàm số \(g\left( t \right) = {t^2} - t + 3\) trên đoạn \(\left[ {0;1} \right]\)

\(g'\left( t \right) = 2t - 1\)

\(g'\left( t \right) = 0 \Leftrightarrow t = {1 \over 2}\)

Ta có: \(g\left( 0 \right) = 3;g\left( {{1 \over 2}} \right) = {{11} \over {14}};g\left( 1 \right) = 3\)

Do đó:  \(\mathop {\min g\left( t \right)}\limits_{t \in \left[ {0;1} \right]}  = {{11} \over {14}};\mathop {\max g\left( t \right)}\limits_{t \in \left[ {0;1} \right]}  = 3\)

Vậy: \(\mathop {\min f\left( x \right)}\limits_{x \in {\mathbb{R}}}  = {{11} \over {14}}\) đạt được khi \({\sin ^2}x = \frac{1}{2} \) \(\Leftrightarrow \frac{{1 - \cos 2x}}{2} = \frac{1}{2}  \) \(\Leftrightarrow 1 - \cos 2x = 1 \) \( \Leftrightarrow \cos 2x = 0  \) \(\Leftrightarrow 2x = \frac{\pi }{2} + k\pi  \) \(  \Leftrightarrow x = \frac{\pi }{4} + \frac{{k\pi }}{2}\)

\(\mathop {\max f\left( x \right)}\limits_{x \in {\mathbb{R}}}  = 3\) đạt được khi \( x = \frac{k\pi }{2} \)

LG d

\(f\left( x \right) = x - \sin 2x\) trên đoan \(\left[ { - {\pi  \over 2};\pi } \right]\).

Lời giải chi tiết:

\(f'\left( x \right) = 1 - 2\cos 2x;\)

\(f'\left( x \right) = 0 \Leftrightarrow \cos 2x = {1 \over 2} = \cos {\pi  \over 3}\) \( \Leftrightarrow 2x =  \pm {\pi  \over 3} + k2\pi \) \( \Leftrightarrow x =  \pm {\pi  \over 6} + k\pi ,k \in {\mathbb{Z}}\)

Với \( - {\pi  \over 2} < x < \pi ,f'\left( x \right) = 0\) tại các điểm \( - {\pi  \over 6},{\pi  \over 6}\) và \({{5\pi } \over 6}\)

Ta có \(f\left( { - {\pi  \over 6}} \right) =  - {\pi  \over 6} + {{\sqrt 3 } \over 2};\) \(f\left( {{\pi  \over 6}} \right) = {\pi  \over 6} - {{\sqrt 3 } \over 2};\) \(f\left( {{{5\pi } \over 6}} \right) = {{5\pi } \over 6} + {{\sqrt 3 } \over 2}\); \(f\left( { - {\pi  \over 2}} \right) =  - {\pi  \over 2};f\left( \pi  \right) = \pi \)
So sánh năm giá trị trên ta được:
\(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - {\pi  \over 2};\pi } \right]}  = {{5\pi } \over 6} + {{\sqrt 3 } \over 2}\) và \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - {\pi  \over 2};\pi } \right]}  =  - {\pi  \over 2}\)

Loigiaihay.com