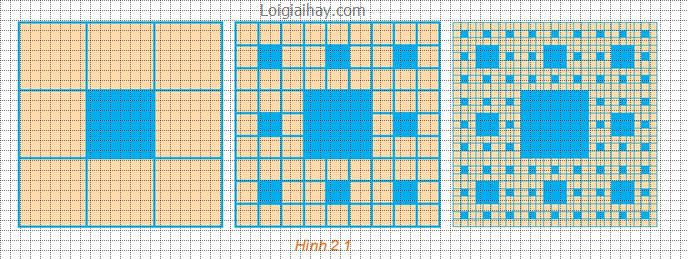
Bài 2.32 trang 57 SGK Toán 11 tập 1 - Kết nối tri thứcMột hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa lại được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần thì tổng diện tích các hình vuông được tô màu xanh bao nhiêu? Quảng cáo
Đề bài Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa lại được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần thì tổng diện tích các hình vuông được tô màu xanh bao nhiêu? Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào dữ liệu đề bài, lần lượt suy ra công thức tính tương ứng. Lời giải chi tiết Diện tích ô vuông màu xanh sau lần phân chia thứ nhất là \(\frac{1}{9}\), số ô vuông màu xanh được tạo thêm là \({8^0}\). Diện tích ô vuông màu xanh sau lần phân chia thứ hai là \(\frac{1}{{{9^2}}}\), số ô vuông màu xanh được tạo thêm là \({8^1}\). Diện tích ô vuông màu xanh sau lần phân chia thứ ba là \(\frac{1}{{{9^3}}}\), số ô vuông màu xanh được tạo thêm là \({8^2}\). Diện tích ô vuông màu xanh sau lần phân chia thứ tư là \(\frac{1}{{{9^4}}}\), số ô vuông màu xanh được tạo thêm là \({8^3}\). Diện tích ô vuông màu xanh sau lần phân chia thứ năm là \(\frac{1}{{{9^5}}}\), số ô vuông màu xanh được tạo thêm là \({8^4}\). Tổng diện tích các ô vuông màu xanh là: \(\frac{1}{9} + \frac{1}{{{9^2}}} \times {8^1} + \frac{1}{{{9^3}}} \times {8^2} + \frac{1}{{{9^4}}} \times {8^3} + \frac{1}{{{9^5}}} \times {8^4} = 0,445\).
|




















Danh sách bình luận