Bài 23 trang 66 SGK Toán 7 tập 2Cho G là trọng tâm của tam giác Quảng cáo
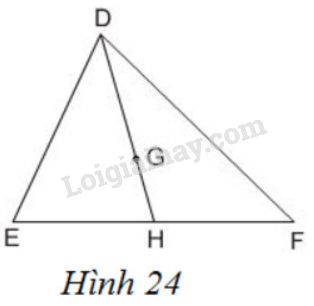
Đề bài Cho \(G\) là trọng tâm của tam giác \(DEF\) với đường trung tuyến \(DH\). Trong các khẳng định sau đây, khẳng định nào đúng ? \(\dfrac{DG}{DH}= \dfrac{1}{2}\); \(\dfrac{DG}{GH}= 3\) \(\dfrac{GH}{DH}= \dfrac{1}{3}\); \(\dfrac{GH}{DG}= \dfrac{2}{3}\)
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm ấy cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy. Lời giải chi tiết \(G\) là trọng tâm của tam giác \(DEF\), đường trung tuyến \(DH\). Ta có: \(\dfrac{{DG}}{{DH}} = \dfrac{2}{3}\) nên ta gọi \(DG = 2a;DH = 3a\left( {a > 0} \right)\) \(\Rightarrow\) \(GH=DH-DG=3a-2a=a\) Do đó: \(\begin{array}{l} Vậy khẳng định \(\dfrac{GH}{DH}= \dfrac{1}{3}\) là đúng. Các khẳng định còn lại sai.
|




















Danh sách bình luận