Bài 27 trang 67 SGK Toán 7 tập 2Hãy chứng minh định lí đảo của định lí Quảng cáo
Đề bài Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Chứng minh tam giác \(ABC\) cân tại \(A\) ta chứng minh \(\widehat B = \widehat C\) hoặc \(AB = AC.\) Lời giải chi tiết Ta đưa về bài toán: Cho \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G.\) Biết \(BM=CN\), chứng minh tam giác \(ABC\) là tam giác cân.
Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\) \(\Rightarrow \) \(G\) là trọng tâm của tam giác \(ABC\). \(\Rightarrow GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\). Mà \(BM = CN\) (giả thiết) nên \(GB = GC.\) Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\). \(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (Tính chất tam giác cân). Xét \(∆BCN\) và \(∆CBM\) có: +) \(BC\) là cạnh chung +) \(CN = BM\) (giả thiết) +) \(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên) Suy ra \(∆BCN = ∆CBM\) (c.g.c) \(\Rightarrow \) \(\widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng). \(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân) (điều phải chứng minh). Loigiaihay.com
|














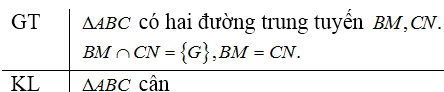







Danh sách bình luận