Bài 22 trang 28 SGK Hình học 12 Nâng caoCho khối lăng trụ tam giác đều ABC.A'B’C. Gọi M là trung điểm của AA’. Mặt phẳng đi qua M, B’, C chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó. Quảng cáo
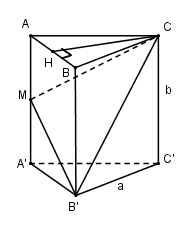
Đề bài Cho khối lăng trụ tam giác đều \(ABC.A'B’C\). Gọi \(M\) là trung điểm của \(AA’\). Mặt phẳng đi qua \(M, B’, C\) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó. Phương pháp giải - Xem chi tiết +) Tính thể tích khối chóp C.ABB'M. - Kẻ đường cao CH của tam giác ABC. - Chứng minh \(CH\bot(ABB'M)\). - Tính thể tích khối chóp \(V = \frac{1}{3}Sh\) +) Tính thể tích khối lăng trụ ABC.A'B'C'. \(V = Bh\) +) Tính thể tích khối đa diện còn lại và suy ra tỉ số. Lời giải chi tiết
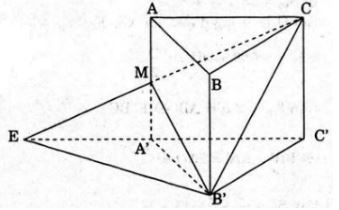
Gọi độ dài cạnh đáy của lăng trụ là \(a\), độ dài cạnh bên của lăng trụ là \(b\). Ta có: \(\left\{ \begin{array}{l}CH \bot AB\\CH \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right)\end{array} \right.\) \( \Rightarrow CH \bot \left( {ABB'A'} \right)\) \( \Rightarrow CH \bot \left( {ABB'M} \right)\). \( \Rightarrow {V_{C.ABB'M}} = \frac{1}{3}CH.{S_{ABB'M}}\) +) \(CH = \sqrt {A{C^2} - A{H^2}} \) \( = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\) +) Diện tích hình thang \(ABB’M\) là: \({S_{ABB'M}} = {1 \over 2}\left( {AM + BB'} \right)AB\) \( = {1 \over 2}\left( {{b \over 2} + b} \right).a = {{3ab} \over 4}\) Thể tích khối chóp \(C.ABB’M\) là: \({V_{C.ABB'M}} = {1 \over 3}{S_{ABB'M}}.CH \) \(= {1 \over 3}{{3ab} \over 4}.{{a\sqrt 3 } \over 2} = {{{a^2}b\sqrt 3 } \over 8}\) Lại có \({S_{ABC}} = \frac{1}{2}CH.AB\)\( = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a = \frac{{{a^2}\sqrt 3 }}{4}\) Vậy thể tích khối lăng trụ là: \({V_{ABC.A'B'C'}} = {S_{ABC}}.AA' \) \(= {{{a^2}\sqrt 3 } \over 4}.b = {{{a^2}b\sqrt 3 } \over 4} \) \(\begin{array}{l} Chú ý: Có thể chứng minh được hai khối chóp \(C.ABB’M\) và \(B’A’C’CM\) có cùng chiều cao và có diện tích đáy bằng nhau nên chúng có thể tích bằng nhau. Cách khác: Gọi V, S, h lần lượt là thể tích và diện tích đáy, chiều cao của lăng trụ: V= S.h. V1,V2 lần lượt là thể tích phần lăng trụ bên trên, bên dưới thiết diện MB’C E = CM ∩ C'A', do M là trung điểm của AA’ nên A’E = A’C’ SΔEA'B'=SΔA'B'C' =S Ta có:
Loigiaihay.com
|














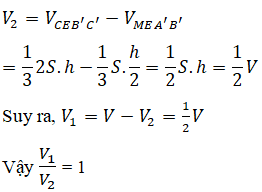






Danh sách bình luận