Bài 21 trang 23 Sách giáo khoa (SGK) Hình học 10 Nâng caoCho tam giác vuông cân OAB với OA = OB = a. Hãy dựng các vec tơ sau đây và tính độ dài của chúng Quảng cáo
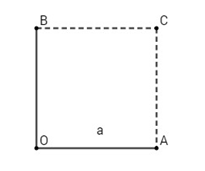
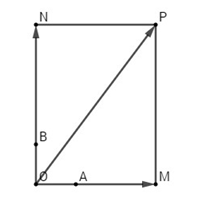
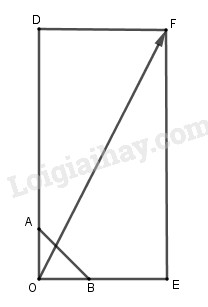
Đề bài Cho tam giác vuông cân \(OAB\) với \(OA = OB = a\). Hãy dựng các vec tơ sau đây và tính độ dài của chúng \(\eqalign{ Lời giải chi tiết +) Vẽ hình vuông \(OACB\), ta có \(\eqalign{ Theo định lí Pitago trong tam giác OAC có: \(OC = \sqrt {O{A^2} + A{C^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) Mà OACB là hình vuông nên BA=OC=\(a\sqrt 2 \) Vậy \(\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = a\sqrt 2 = \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right|\) Cách khác: Vẽ hình vuông \(OACB\), gọi M là trung điểm AB. Khi đó \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} = 2\overrightarrow {OM}\) \( \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = 2\left| {\overrightarrow {OM} } \right|=2OM\) Mà OM là trung tuyến trong tam giác vuông OAB nên \(OM = \frac{1}{2}AB = \frac{1}{2}\sqrt {O{A^2} + O{B^2}} \)\(= \frac{1}{2}\sqrt {{a^2} + {a^2}} = \frac{{a\sqrt 2 }}{2}\) \( \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = 2OM \)\(= 2.\frac{{a\sqrt 2 }}{2} = a\sqrt 2 \). +) Gọi \(M, N\) là điểm thỏa mãn \(\overrightarrow {OM} = 3\overrightarrow {OA} ,\,\overrightarrow {ON} = 4\overrightarrow {OB} \). Vẽ hình chữ nhật \(MONP\), ta có \(\eqalign{ +) Dựng điểm D, E sao cho \(\overrightarrow {OD} = \frac{{21}}{4}\overrightarrow {OA} ,\) \(\overrightarrow {OE} = 2,5\overrightarrow {OB} \)
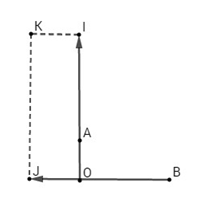
Dựng hình chữ nhật ODFE ta có: \(\frac{{21}}{4}\overrightarrow {OA} + 2,5\overrightarrow {OB} \) \( = \overrightarrow {OD} + \overrightarrow {OE} = \overrightarrow {OF} \) \(\begin{array}{l} \Rightarrow \left| {\frac{{21}}{4}\overrightarrow {OA} + 2,5\overrightarrow {OB} } \right| = \left| {\overrightarrow {OF} } \right|\\ = \sqrt {O{E^2} + E{F^2}} = \sqrt {O{E^2} + O{D^2}} \\ = \sqrt {{{\left( {2,5OB} \right)}^2} + {{\left( {\frac{{21}}{4}OA} \right)}^2}} \\ = \sqrt {{{\left( {2,5a} \right)}^2} + {{\left( {\frac{{21}}{4}a} \right)}^2}} = \frac{{\sqrt {541} a}}{4}\end{array}\) +) Gọi \(I, J\) là điểm thỏa mãn \(\overrightarrow {OI} = {{11} \over 4}\overrightarrow {OA} ,\,\overrightarrow {OJ} = - {3 \over 7}\overrightarrow {OB} \)
Vẽ hình chữ nhật \(OIKJ\), ta có \(\eqalign{ Loigiaihay.com
|




















Danh sách bình luận