Bài 20 trang 90 SGK Hình học 10 Nâng caoCho hai đường thẳng sau: Quảng cáo
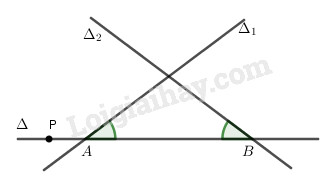
Đề bài Cho hai đường thẳng \(\eqalign{ Viết phương trình đường thẳng \(\Delta \) đi qua điểm P(3, 1) và cắt \({\Delta _1},{\Delta _2}\) lần lượt ở A,B sao cho \({\Delta}\) tạo với \({\Delta _1}\) và \({\Delta _2}\) một tam giác cân có cạnh đáy là AB. Phương pháp giải - Xem chi tiết \(\Delta \) cắt \({\Delta _1},{\Delta _2}\) ở A và B sao cho \({\Delta}\) tạo với \({\Delta _1}\) và \({\Delta _2}\) một tam giác cân có đáy AB thì góc hợp bởi \(\Delta \) với \({\Delta _1}\) và góc hợp bởi \(\Delta \) với \({\Delta _2}\) bằng nhau. Do đó, cách làm như sau: +) Giả sử \(\Delta \) qua P có vectơ pháp tuyến \(\overrightarrow n \left( {a;b} \right)\). +) Tính \(\cos \left( {\Delta ,{\Delta _1}} \right) \) và \(\cos \left( {\Delta ,{\Delta _2}} \right)\) +) Tìm mối quan hệ của a, b từ phương trình \(\cos \left( {\Delta ,{\Delta _1}} \right) = \cos \left( {\Delta ,{\Delta _2}} \right)\). +) Chọn b=1, tìm a và suy ra phương trình đường thẳng. Lời giải chi tiết \({\Delta _1}\) có vectơ pháp tuyến là: \(\overrightarrow {{n_1}} \left( {1;2} \right).\) \({\Delta _2}\) có vectơ pháp tuyến là: \(\overrightarrow {{n_2}} \left( {3; - 1} \right).\) Giả sử \(\Delta \) qua P có vectơ pháp tuyến \(\overrightarrow n \left( {a;b} \right)\). Từ hình vẽ ta thấy: \(\Delta \) cắt \({\Delta _1},{\Delta _2}\) ở A và B sao cho \({\Delta}\) tạo với \({\Delta _1}\) và \({\Delta _2}\) một tam giác cân có đáy AB thì góc hợp bởi \(\Delta \) với \({\Delta _1}\) và góc hợp bởi \(\Delta \) với \({\Delta _2}\) bằng nhau. Do đó, \(\cos \left( {\Delta ,{\Delta _1}} \right) = \cos \left( {\Delta ,{\Delta _2}} \right)\) \(\eqalign{ Chọn \(b = 1\) ta có: \({a^2} - 2a - 1 = 0 \Leftrightarrow a = 1 \pm \sqrt 2 \) Loigiaihay.com
|





















Danh sách bình luận