Bài 20 trang 122 SGK Toán 8 tập 1Vẽ hình chữ nhật có một cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Quảng cáo
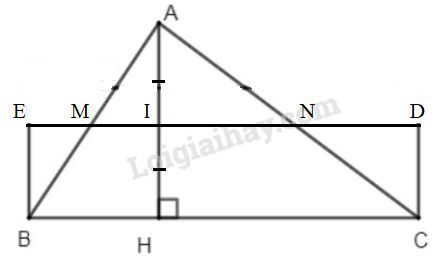
Đề bài Vẽ hình chữ nhật có một cạnh bằng một cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó. Lời giải chi tiết Cho tam giác \(ABC\) với đường cao \(AH\) Gọi \(M, N, I\) là trung điểm của \(AB, AC, AH.\) Lấy \(E\) đối xứng với \(I\) qua \(M, D\) đối xứng với \(I\) qua \(N.\) \(⇒\) Hình chữ nhật \(BEDC\) là hình cần dựng.
Thật vậy: Vì \(E\) đối xứng với \(I\) qua \(M\) nên \(M\) là trung điểm của \(EI\) Do đó, \(EM=MI\) Xét hai tam giác \(∆EBM\) và \(∆IAM\) có: +) \(MA=MB\) (do M là trung điểm của AB) +) \(\widehat {BME} = \widehat {AMI}\) (đối đỉnh) +) \(EM=MI\) (chứng minh trên) \( \Rightarrow ∆EBM = ∆IAM\) ( c-g-c) \( \Rightarrow {S_{IAM}} = {S_{EBM}}\) Vì \(D\) đối xứng với \(I\) qua \(N\) nên \(N\) là trung điểm của \(DI\) Do đó, \(NI=ND\) Xét hai tam giác \(∆IAN\) và \(∆DCN\) có: +) \(IN=ND\) (chứng minh trên) +) \(\widehat {ANI} = \widehat {DNC}\) (đối đỉnh) +) \(AN = NC \) (do N là trung điểm của AC) \( \Rightarrow ∆IAN = ∆DCN\) ( c-g-c) \( \Rightarrow {S_{DCN}} = {S_{IAN}}\) Ta có: \({S_{BEM}} + {S_{BMNC}} + {S_{N{\rm{D}}C}} = {S_{AMI}} \)\(+ {S_{BMNC}} + {S_{AIN}}\) \(\Rightarrow {S_{ABC}}={S_{EB{\rm{D}}C}} \)\( =BE.BC= \dfrac{1}{2}AH.BC \) (vì \(BE=IH=\dfrac{AH}2)\) Ta đã tìm được công thức tính diện tích tam giác bằng một phương pháp khác. Chú ý: Theo cách dựng trên ta có \(BEDC\) là hình chữ nhật vì: +) MN là đường trung bình của tam giác ABC nên \(MN//BC\) hay \(ED//BC\) +) Vì \(∆EBM = ∆IAM\) nên \(\widehat {EBM}=\widehat{MAI}\) mà hai góc này ở vị trí so le trong nên \(EB//AI\) hay \(EB//AH\) +) Vì \(∆IAN = ∆DCN\) nên \(\widehat {DCN}=\widehat{NAI}\) mà hai góc này ở vị trí so le trong nên \(DC//AI\) Do đó \(EB//DC\) và \(ED//BC\) nên \(BEDC\) là hình bình hành Mà \(AH\bot BC, EB//AH\) nên \(EB\bot BC,\) suy ra \(BEDC\) là hình chữ nhật. Loigiaihay.com
|




















Danh sách bình luận