Bài 18 trang 110 SGK Toán 9 tập 1Khoảng cách từ tâm A đến trục Ox là 4. Vậy d>R, do đó đường tròn và trục Ox không giao nhau. Quảng cáo
Đề bài Trên mặt phẳng tọa độ \(Oxy\), cho điểm \(A(3;4)\). Hãy xác định vị trí tương đối của đường tròn \((A;3)\) và các trục tọa độ. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Cho đường tròn \((O;R)\) và đường thẳng \(a\), gọi \(d=OH\) là khoảng cách từ \(a\) đến tâm \(O\). Khi đó: +) \(a\) và \((O)\) không giao nhau nếu \(d > R\). +) \(a\) và \((O)\) tiếp xúc nhau nếu \(d = R\); Lời giải chi tiết
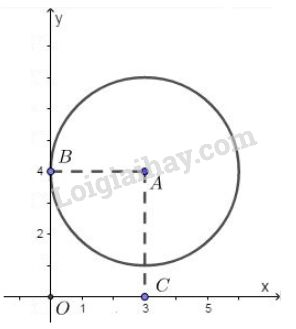
+) Đường tròn \((A;\ 3)\) có tâm \(A\) và bán kính \(R=3\). Kẻ \(AC\bot Ox, AB \bot Oy\) (hình vẽ) +) Khoảng cách từ tâm \(A\) đến trục \(Ox\) là \(AC=4\). Vì \(4 > 3 \Rightarrow AC > R\). Suy ra đường tròn \((A;\ 3)\) và trục \(Ox\) không cắt nhau. +) Khoảng cách từ tâm \(A\) tới trục \(Oy\) là \(AB=3\). Suy ra \(AB=R\,(=3)\) do đó đường tròn \((A;\ 3)\) và trục \(Oy\) tiếp xúc nhau. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
