Bài 17 trang 80 Tài liệu dạy – học Toán 9 tập 2Giải bài tập Trên đường tròn (O; R) lấy 4 điểm theo thứ tự A, B, C, D sao cho Quảng cáo
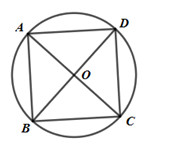
Đề bài Trên đường tròn (O; R) lấy 4 điểm theo thứ tự A, B, C, D sao cho \(cung\,AB = cung\,BC = cung\,CD = cung\,DA.\) a) Chứng minh rằng tứ giác ABCD là một hình vuông. b) Tính cạnh của hình vuông theo R. Phương pháp giải - Xem chi tiết a) Chứng minh ABCD là hình thoi có 1 góc vuông. b) Áp dụng định lí Pytago trong tam giác vuông. Lời giải chi tiết a) Ta có: \(cung\,AB = cung\,BC = cung\,CD = cung\,DA \) \(\Rightarrow AB = BC = CD = DA \Rightarrow \) ABCD là hình thoi. Xét tam giác ABC có \(BO = \dfrac{1}{2}AC = R \Rightarrow \Delta ABC\) vuông tại B (Trung tuyến ứng với một cạnh bằng nửa cạnh ấy) \( \Rightarrow \widehat {ABC} = {90^0} \Rightarrow ABCD\) là hình vuông (Hình thoi có 1 góc vuông). b) Vì ABCD là hình vuông \( \Rightarrow AC \bot BD \Rightarrow \Delta OAB\) vuông tại O. Lại có \(OA = OB = R\). Áp dụng định lí Pytago ta có : \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{R^2} + {R^2}} \)\(\, = \sqrt {2{R^2}} = R\sqrt 2 \). Loigiaihay.com
|




















Danh sách bình luận