Bài 15 trang 80 Tài liệu dạy – học Toán 9 tập 2

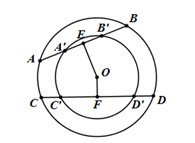
Đề bài

Cho hai đường tròn đồng tâm (O; R), (O; R’) với (R > R’), dây AB và CD của đường tròn (O; R) cắt đường tròn (O; R’) lần lượt tại A’, B’ và C’, D’. Chứng minh rằng nếu hai cung AB, CD bằng nhau thì hai cung A’B’, C’D’ cũng bằng nhau.

Lời giải chi tiết

 

Gọi E, F lần lượt là trung điểm của AB và CD \( \Rightarrow OE \bot AB;\,\,OF \bot CD\) (quan hệ vuông góc giữa đường kính và dây cung).

\( \Rightarrow OE \bot A'B';\,\,OF \bot C'D'\).

\( \Rightarrow E;F\) lần lượt là trung điểm của A’B’ và C’D’.

Xét đường tròn \(\left( O \right)\) có: \(AB = CD \Rightarrow OE = OF\) (hai dây bằng nhau thì cách đều tâm).

Xét đường tròn tâm \(\left( {O'} \right)\) có \(OE = OF \Rightarrow A'B' = C'D'\) (hai dây cách đều tâm thì bằng nhau).

 Loigiaihay.com