Bài 19 trang 80 Tài liệu dạy – học Toán 9 tập 2

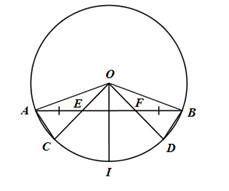
Đề bài

Cho (O) và dây AB của đường tròn O. Trên AB lấy hai điểm E và F sao cho AE = BF. Tia OE và tia OF cắt (O) lần lượt tại C và D.

a) Chứng minh sđ cung AC = sđ cung BD .

b) Gọi I là điểm chính giữa cung AB.Chứng minh I là điểm chính giữa cung CD.

Lời giải chi tiết

 

a) Xét tam giác OAB có \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow \widehat {OAB} = \widehat {OBA}\) (hai góc ở đáy của tam giác cân).

Xét tam giác OAE và tam giác OBF có:

\(\begin{array}{l}OA = OB = R;\\\widehat {OAB} = \widehat {OBA}\,\,\left( {cmt} \right);\\AE = BF\,\,\left( {gt} \right)\\ \Rightarrow \Delta OAE = \Delta OBF\,\,\left( {c.g.c} \right)\\ \Rightarrow OE = OF\end{array}\)

\(\Delta OEF\) cân tại O \( \Rightarrow \widehat {OEF} = \widehat {OFE}\).

Ta lại có: \(\widehat {AEC} = \widehat {OEF}\,\,\,\left( {dd} \right);\,\,\widehat {BFD} = \widehat {OFE}\,\,\left( {dd} \right)\)

\(\Rightarrow \widehat {AEC} = \widehat {BFD}\)

Ta có: \(OC = OD = R;\,\,OE = OF\,\,\left( {cmt} \right)\) \( \Rightarrow EC = FD\)

Xét tam giác AEC và tam giác BFD có :

\(\begin{array}{l}AE = BF\,\,\left( {gt} \right);\\\widehat {AEC} = \widehat {BFD}\,\,\left( {cmt} \right);\\EC = FD\,\,\left( {cmt} \right)\end{array}\)

\( \Rightarrow \Delta AEC = \Delta BFD\,\,\left( {c.g.c} \right)\)

\(\Rightarrow AC = BD \)

\(\Rightarrow cung\,AC = cung\,BD\) (hai dây bằng nhau căng hai cung bằng nhau).

b) Vì \(\Delta OAE = \Delta OBF\,\,\left( {cmt} \right)\)

\(\Rightarrow \widehat {AOE} = \widehat {BOF}\,\,\left( 1 \right)\) (2 góc tương ứng).

Vì I là điểm chính giữa cung AB \( \Rightarrow cung\,AI = cung\,BI \) \(\Rightarrow \widehat {AOI} = \widehat {BOI}\,\,\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow \widehat {COI} = \widehat {DOI} \) \(\Rightarrow sdcung\,CI = sd\,cung\,DI \) \(\Rightarrow cung\,CI = cung\,DI\).

Vậy I là điểm chính giữa của cung CD.

 Loigiaihay.com