Bài 13 trang 120 SGK Hình học 10 Nâng caoChứng minh rằng đường thẳng IM cắt parabol đã cho tại một điểm duy nhất. Quảng cáo
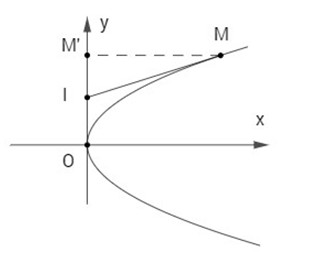
Đề bài Cho parabol \((P):{y^2} = 2px.\) Với mỗi điểm M trên (P) (M khác O), gọi M’ là hình chiếu của M trên Oy và I là trung điểm của đoạn OM’. Chứng minh rằng đường thẳng IM cắt parabol đã cho tại một điểm duy nhất. Lời giải chi tiết
Giả sử \(M({x_o}\,;\,{y_o})\,\, \in \,\,\,(P)\) ta có \(y_o^2 = 2p{x_o}\,({x_o} \ne 0)\). M’ là hình chiếu của M trên Oy nên \(M'(0\,;\,{y_o})\), khi đó \(I\left( {0\,;\,{{{y_o}} \over 2}} \right)\) \( \Rightarrow \,\,\overrightarrow {IM} = \left( {{x_o}\,;\,{{{y_o}} \over 2}} \right)\) là vectơ chỉ phương của đường thẳng IM. IM đi qua \(I\left( {0\,;\,{{{y_o}} \over 2}} \right)\) và nhận \(\overrightarrow {IM} = \left( {{x_o}\,;\,{{{y_o}} \over 2}} \right)\) nên phương trình tham số là \(\left\{ \matrix{ Thay x, y trong phương trình tham số của IM vào phương trình của (P) ta được \(\begin{array}{l} Mà \(2p{x_o} = y_o^2\) nên \(\frac{{y_0^2}}{4}{\left( {1 + t} \right)^2} = y_0^2t \) \(\Leftrightarrow y_o^2(1 + {t})^2 = 4y_o^2t \Leftrightarrow (1 + {t})^2 = 4t\,\,\) ( do \({y_o} \ne 0\)) \( \Leftrightarrow 1 + 2t + {t^2} - 4t = 0 \) \(\Leftrightarrow {t^2} - 2t + 1 = 0 \) \(\Leftrightarrow {\left( {t - 1} \right)^2} = 0 \Leftrightarrow t = 1\) Vậy IM cắt (P) tại điểm duy nhất \(M({x_o}\,;\,{y_o})\,\) . Loigiaihay.com
|