Bài 12 trang 119 SGK Hình học 10 Nâng caoViết phương trình chính tắc của hypebol (H) nhận các tiêu điểm của (E) làm đỉnh và có hai tiêu điểm là hai đỉnh của elip (E) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
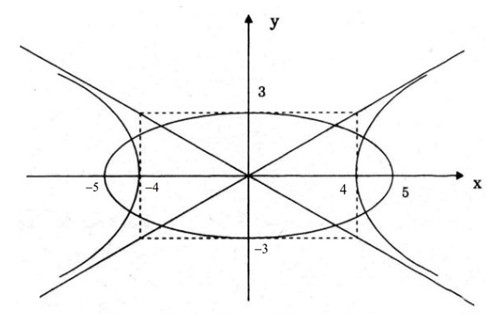
Cho elip \((E):{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1.\) LG a Xác định tọa độ hai tiêu điểm và các đỉnh của (E). Lời giải chi tiết: Ta có: \(a = 5\,,\,\,\,b = 3\,,\,\,c = \sqrt {{a^2} - {b^2}} = 4\) Tọa độ các tiêu điểm của (E) là \({F_1}\,( - 4\,;\,0)\,,\,\,{F_2}\,(4\,;\,0)\) . Tọa độ các đỉnh của (E) là \({A_1}( - 5\,;\,0)\,,\,\,{A_2}(5\,;\,0)\,,\,\,{B_1}(0\,;\, - 3)\,,\,\,{B_2}(0\,;\,3)\) . LG b Viết phương trình chính tắc của hypebol (H) nhận các tiêu điểm của (E) làm đỉnh và có hai tiêu điểm là hai đỉnh của elip (E). Lời giải chi tiết: (H) nhận (-4, 0) và (4, 0) làm đỉnh thì \(a=4\). (H) nhận (-5, 0) và (5, 0) làm tiêu điểm thì có \(c=5\). \( \Rightarrow \,\,{b^2} = {c^2} - {a^2} = 25 - 16 = 9\,\,\, \Rightarrow \,\,\,b = 3\) Vậy phương trình chính tắc của hypebol (H) là : \({{{x^2}} \over {16}} - {{{y^2}} \over 9} = 1\) LG c Vẽ phác elip (E) và hypebol (H) nói ở câu b) trong cùng một hệ trục tọa độ. Lời giải chi tiết: Vẽ (E) và (H).
LG d Viết phương trình của đường tròn đi qua các giao điểm của hai đường cônic nói trên. Lời giải chi tiết: Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình \(\left\{ \matrix{ Vậy (E) và (H) cắt nhau tại 4 điểm có tọa độ thỏa phương trình \({x^2} + {y^2} = {{881} \over {41}}\) Vậy đường tròn đi qua các giao điểm của (E) và (H) có phương trình là \({x^2} + {y^2} = {{881} \over {41}}\) Loigiaihay.com
|