Bài 12 trang 118 Tài liệu dạy – học toán 6 tập 2Giải bài tập Cho góc bẹt aOb, vẽ tia Ot là phân giác của Quảng cáo
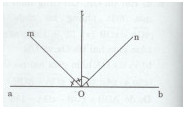
Đề bài Cho góc bẹt aOb, vẽ tia Ot là phân giác của \(\widehat {aOb}\), Om là phân giác của \(\widehat {aOt}\), On là phân giác của \(\widehat {tOb}\). Chứng tỏ \(\widehat {mOn}\) vuông. Lời giải chi tiết Ta có: \(\widehat {aOt} + \widehat {bOt} = {180^0}\) (kề bù) Mà \(\widehat {mOt} = {1 \over 2}\widehat {aOt}\) (Om là tia phân giác của góc aOt) Và \(\widehat {nOt} = {1 \over 2}\widehat {bOt}\) (On là phân giác của góc bOt) Và \(\widehat {mOn} = \widehat {mOt} + \widehat {nOt}\) (tia Ot nằm giữa hai tia Om và On) Do đó: \(\widehat {mOn} = \widehat {mOt} + \widehat {nOt} = {1 \over 2}\widehat {aOt} + {1 \over 2}\widehat {bOt} = {1 \over 2}(\widehat {aOt} + \widehat {bOt}) = {1 \over 2}{.180^0} = {90^0}.\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
