Bài 10 trang 15 SGK Hình học 12 Nâng caoChứng minh rằng : a) Hợp thành của hai phép đối xứng qua hai mặt phẳng song song (P) và (Q) là một phép tịnh tiến ; b) Hợp thành của hai phép đối xứng qua hai mặt phẳng (P) và (Q) vuông góc với nhau là một phép đối xứng qua đường thẳng. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
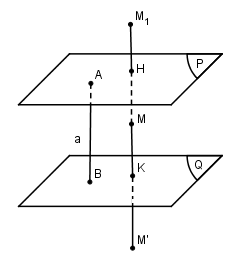
Chứng minh rằng : LG a Hợp thành của hai phép đối xứng qua hai mặt phẳng song song \((P)\) và \((Q)\) là một phép tịnh tiến ; Lời giải chi tiết:
Lấy hai điểm \(A\) và \(B\) lần lượt nằm trên \((P)\) và \((Q)\) sao cho \(AB \bot \left( P \right)\). Khi đó véc tơ AB có hướng không đổi từ (P) đến (Q) và độ lớn của véc tơ AB chính là khoảng cách giữa (P) và (Q). Với một điểm \(M\) bất kì, ta gọi \({M_1}\) là điểm đối xứng với \(M\) qua mp\((P)\) và \(M’\) là điểm đối xứng với \({M_1}\) qua mp\((Q)\). Như vậy \(M’\) là ảnh của \(M\) qua phép hợp thành của phép đối xứng qua mp\((P)\) và phép đối xứng qua mp\((Q)\). \( = 2\left( {\overrightarrow {H{M_1}} + \overrightarrow {{M_1}K} } \right) \) \(= 2\overrightarrow {HK} = 2\overrightarrow {AB} \) LG b Hợp thành của hai phép đối xứng qua hai mặt phẳng \((P)\) và \((Q)\) vuông góc với nhau là một phép đối xứng qua đường thẳng. Lời giải chi tiết:
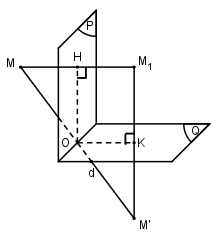
Giả sử \(\left( P \right) \bot \left( Q \right)\) và \(d = \left( P \right) \cap \left( Q \right)\) \(\Rightarrow \left( {M{M_1}M'} \right) \bot d\) \(= \overrightarrow {OH} + \overrightarrow {HM} + \overrightarrow {OK} + \overrightarrow {KM'} \) \(= \left( {\overrightarrow {OH} + \overrightarrow {OK} } \right) + \left( {\overrightarrow {{M_1}H} + \overrightarrow {{M_1}K} } \right) \) \(= \overrightarrow {O{M_1}} + \overrightarrow {{M_1}O} = \overrightarrow 0 \) Vậy phép hợp thành của phép đối xứng qua mp\((P)\) và phép đối xứng qua mp\((Q)\) với \(\left( P \right) \bot \left( Q \right)\) là phép đối xứng qua đường thẳng \(d\). Chú ý: Có thể giải thích như sau: Gọi d = (P) ∩ (Q). M là một điểm bất kì. Giả sử phép đối xứng qua (P) biến M thành M’ và phép đối xứng qua (Q) biến M’ thành M’’. I ∈ (P) và I ∈ (Q) I ∈ d mà d ⊥ MM’’ (do d <=> (Q). Vậy d là đường trung trực của MM’’. Trường hợp M ∈ (Q) nhưng M ∈ d tương tự. Trường hợp 3. Nếu M ∈(P) và M ∈(Q) thì M, M’, M’’ phân biệt. Vì I = (P)∩ (Q) mà (P), (Q) lần lượt là mặt phẳng trung trực của MM’, M’M’’ nên d ⊥ (MM’M’’) => d ⊥ MM'' (*). Mặt khác, gọi I là trung điểm của MM’’, do ΔMM’M’’ vuông tại M’ nên IM = IM’ = IM’’ => I đồng thời thuộc mặt phẳng trung trực của MM’ và M’M’’ hay I ∈(P) và I ∈(Q)=>I ∈d (**) Từ (*), (**) ta có d là đường trung trực của đoạn MM’’ (3) Kết luận: từ (1), (2), (3) ta thấy: nếu thực hiện liên tiếp hai phép đối xứng qua hai mặt phẳng vuông góc (P) và (Q) thì mỗi điểm M ∈ d (với d ∈(P)∩ (Q) biến thành chính nó, mỗi điểm M ∈d biến thành M’’ sao cho d là trung trực của MM’’. Đó chính là phép đối xứng qua đường thẳng d. Loigiaihay.com
|




















Danh sách bình luận