Giải bài 1 trang 77 SGK Giải tích 12

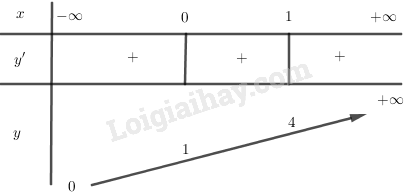
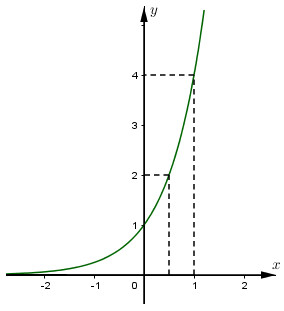
LG a

a) $y = 4^x$;

Phương pháp giải:

Các bước khảo sát và vẽ đồ thị hàm số:

Bước 1: Tập xác định.

Bước 2: Sự biến thiên.

- Tính $y'$, tìm các điểm mà tại đó $y'$ bằng 0 hoặc không xác định.

- Xét dấu $y'$ và suy ra các khoảng đơn điệu của đồ thị hàm số.

- Tính các giới hạn đặc biệt: Giới hạn tại vô cực và giới hạn tại các điểm mà hàm số không xác định.

- Tìm các tiệm cận của đồ thị hàm số (nếu có).

- Lập bảng biến thiên.

Bước 3: Đồ thị.

- Tìm giao điểm của đồ thị hàm số với các trục tọa độ (nếu có).

- Vẽ đồ thị hàm số dựa vào các yếu tố ở trên.

Lời giải chi tiết:

Đồ thị hàm số $y = 4^x$ 

*) Tập xác định: $\mathbb R$

*) Sự biến thiên:

$y' = {4^x}\ln 4 > 0,\forall x \in \mathbb R$

- Hàm số đồng biến trên $\mathbb R$

- Giới hạn đặc biệt:

   $\eqalign{ & \mathop {\lim }\limits_{x \to - \infty } y = 0 \cr  & \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr}$

Tiệm cận ngang: $y=0$.

- Bảng biến thiên:

Đồ thị:

Đồ thị nằm hoàn toàn phía trên trục hoành, cắt trục tung tại điểm $(0;1)$, đi qua điểm $(1;4)$ và qua các điểm $(\dfrac{1}{2}; 2)$, $(-\dfrac{1}{2}; \dfrac{1}{2})$, $(-1; \dfrac{1}{4})$.

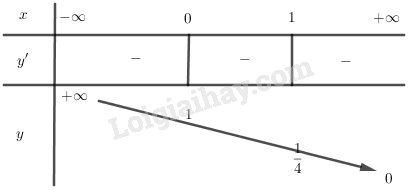
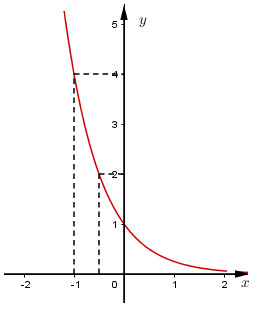
LG b

b) $y= \left ( \dfrac{1}{4} \right )^{x}$.

Phương pháp giải:

Các bước khảo sát và vẽ đồ thị hàm số:

Bước 1: Tập xác định.

Bước 2: Sự biến thiên.

- Tính $y'$, tìm các điểm mà tại đó $y'$ bằng 0 hoặc không xác định.

- Xét dấu $y'$ và suy ra các khoảng đơn điệu của đồ thị hàm số.

- Tính các giới hạn đặc biệt: Giới hạn tại vô cực và giới hạn tại các điểm mà hàm số không xác định.

- Tìm các tiệm cận của đồ thị hàm số (nếu có).

- Lập bảng biến thiên.

Bước 3: Đồ thị.

- Tìm giao điểm của đồ thị hàm số với các trục tọa độ (nếu có).

- Vẽ đồ thị hàm số dựa vào các yếu tố ở trên.

Lời giải chi tiết:

Đồ thị hàm số $y=\left ( \dfrac{1}{4} \right )^{x}$ 

*) Tập xác định: $\mathbb R$

*) Sự biến thiên:

$y' = {\left( {\dfrac{1}{4}} \right)^x}.\ln \left( {\dfrac{1}{4}} \right)$$=  - {\left( {\dfrac{1}{4}} \right)^x}\ln 4 < 0\,\,\forall x \in R$

- Hàm số nghịch biến trên $\mathbb R$

- Giới hạn:

  $\eqalign{ & \mathop {\lim }\limits_{x \to - \infty } y = + \infty \cr  & \mathop {\lim }\limits_{x \to + \infty } y = 0 \cr}$

Tiệm cận ngang $y=0$

- Bảng biến thiên:

*) Đồ thị:

Đồ thị hàm số nằm hoàn toàn về phía trên trục hoành, cắt trục tung tại điểm $(0; 1),$ đi qua điểm $(1; \dfrac{1}{4}$) và qua các điểm $(-\dfrac{1}{2}; 2), (-1;4).$

Loigiaihay.com