Lý thuyết Xác suất thực nghiệm Toán 6 KNTT với cuộc sống

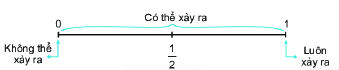
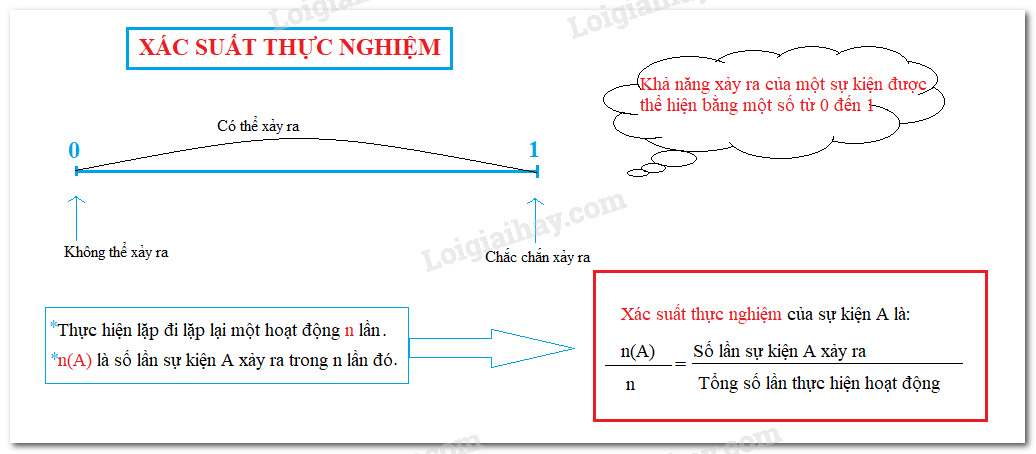
1. Khả năng xảy ra của một sự kiện

Khả năng của một sự kiện được thể hiện bằng một con số từ 0 đến 1.

Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.

Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.

2. Xác suất thực nghiệm

Thực hiện lặp đi lặp lại một hoạt động nào đó n lần.

Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số

\(\frac{{n(A)}}{n} = \) Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động

Được gọi là xác suất thực nghiệm của sự kiện A.

Nhận xét: Xác suất thực nghiệm phụ thuộc vào người thực hiện thí nghiệm, trò chơi và số lần người đó thực hiện thí nghiệm, trò chơi.

Ví dụ:

Vuông gieo một đồng xu 55 lần và thấy có 30 lần xuất hiện mặt sấp. Tròn lấy đồng xu đó gieo 100 lần và thấy có 45 lần xuất hiện mặt sấp.

Hãy tính xác suất thực nghiệm của sự kiện “Đồng xu xuất hiện mặt sấp” trong 2 thí nghiệm trên và so sánh hai xác suất thực nghiệm đó.

Giải:

Vuông:

Số lần gieo được mặt sấp là 30. Tổng số lần gieo là 55 nên xác suất thực nghiệm của sự kiện “Đồng xu xuất hiện mặt sấp”  là: \(\dfrac{{30}}{{55}}\).

Tròn:

Số lần gieo được mặt sấp là 45, tổng số lần gieo là 100. Xác suất thực nghiệm của sự kiện “Đồng xu xuất hiện mặt sấp”  là: \(\dfrac{{45}}{{100}}\).

Ta thấy Vuông và Tròn thực hiện hai thí nghiệm với tổng số lần gieo khác nhau và nhận được xác suất thực nghiệm của sự kiện “Đồng xu xuất hiện mặt sấp”  là khác nhau.

3. Tính xác suất thực nghiệm

Phương pháp:

Bước 1: Xác định số lần được kết quả A (kết quả cần tính xác suất) và tổng số lần gieo.

Bước 2: Sử dụng công thức sau để tính xác suất:

\(\frac{{n(A)}}{n} = \) Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động

Ví dụ:  Gieo một con xúc xắc sáu mặt 7 lần và số chấm xuất hiện của mỗi lần gieo như sau:

Bước 1: Số lần gieo được mặt 3 chấm là 2 lần. Tổng số lần gieo là 7.

Bước 2: Xác suất mặt 3 chấm xuất hiện là \(\dfrac{2}{7}\)

4. Bài tập về Xác suất thực nghiệm

Bài 1. Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:

Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.

A. 0,21

B. 0,44

C. 0,42

D. 0,18

Lời giải: Tổng số lần gieo là 50.

Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.

Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.

Số lần được mặt có số lẻ chấm là 8+3+10=21 lần

Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:

\(\dfrac{{21}}{{50}} = 0,42\)

Chọn đáp án C

Bài 2. Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?

A. \(\dfrac{7}{{11}}\)

B. \(\dfrac{4}{{11}}\)

C. \(\dfrac{4}{7}\)

D. \(\dfrac{3}{7}\)

Lời giải:

Tổng số lần gieo là 22.

Số lần gieo được mặt N là 14.

Xác suất thực nghiệm xuất hiện mặt N là: \(\dfrac{{14}}{{22}} = \dfrac{7}{{11}}\)

Chọn đáp án A.

Bài 3. Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?

A. \(\dfrac{2}{5}\)

B. \(\dfrac{1}{5}\)

C. \(\dfrac{3}{5}\)

D. \(\dfrac{3}{4}\)

Lời giải:

Tổng số lần gieo là 30.

Số lần gieo được mặt S là 30-12=18.

Xác suất thực nghiệm xuất hiện mặt S là: \(\dfrac{{18}}{{30}} = \dfrac{3}{5}\)

Chọn đáp án C.

Bài 4. Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng

A. 0,15

B. 0,3

C. 0,6

D. 0,36

Lời giải: Tổng số lần gieo là 20, số lần xuất hiện mặt 3 chấm là 6 lần.

Xác suất thực nghiệm xuất hiện mặt 3 chấm bằng \(\dfrac{6}{{20}} = 0,3\).

Chọn đáp án B.