Lý thuyết tính chất ba đường cao của tam giácA. KIẾN THỨC CƠ BẢN Quảng cáo
I. Các kiến thức cần nhớ 1. Định nghĩa Đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó. Mỗi tam giác có ba đường cao. 2. Tính chất ba đường cao của tam giác Định lí: Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác
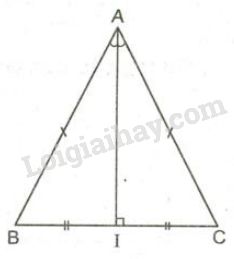
3. Vẽ đường cao, trung tuyến, trung trực, phân giác của tam giác cân. Tính chất: Trong một tam giác cân, đường trung trực ứng với cạnh đáy cũng đồng thời là đường phân giác, đường trung tuyến và đường cao của tam giác đó. Nhận xét: Trong một tam giác, nếu có hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường trung trực, đường cao) trùng nhau thì tam giác đó là tam giác cân.
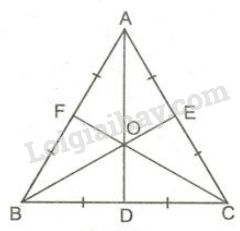
4. Đặc biệt đối với tam giác đều
Hệ quả: Trong một tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau. II. Các dạng toán thường gặp Dạng 1: Chứng minh hai đường thẳng vuông góc Phương pháp: Sử dụng tính chất trực tâm của tam giác. Nếu \(H\) là giao điểm của hai đường cao kẻ từ \(B\) và \(C\) của \(\Delta ABC\) thì \(AH \bot BC.\) Dạng 2: Bài toán về đường cao với tam giác, tam giác cân, tam giác đều Phương pháp: - Sử dụng tính chất vuông góc của đường cao đối với cạnh đối diện - Sử dụng định lý “Trong một tam giác cân, đường cao ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường trung trực của tam giác đó” để một trong các đường trung tuyến, phân giác, đường cao, đường trung trực ứng với cạnh đáy cũng là các đường còn lại. - Sử dụng nhận xét: Trong một tam giác, nếu có hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường trung trực, đường cao) trùng nhau thì tam giác đó là tam giác cân. Dạng 3: Chứng minh ba đường thẳng đồng quy Phương pháp: Nếu ba đường thẳng là ba đường cao của tam giác thì chúng cùng đi qua một điểm.
|