Lý thuyết Thứ tự trong tập hợp các số tự nhiên Toán 6 KNTT với cuộc sống

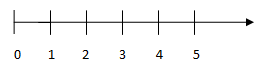
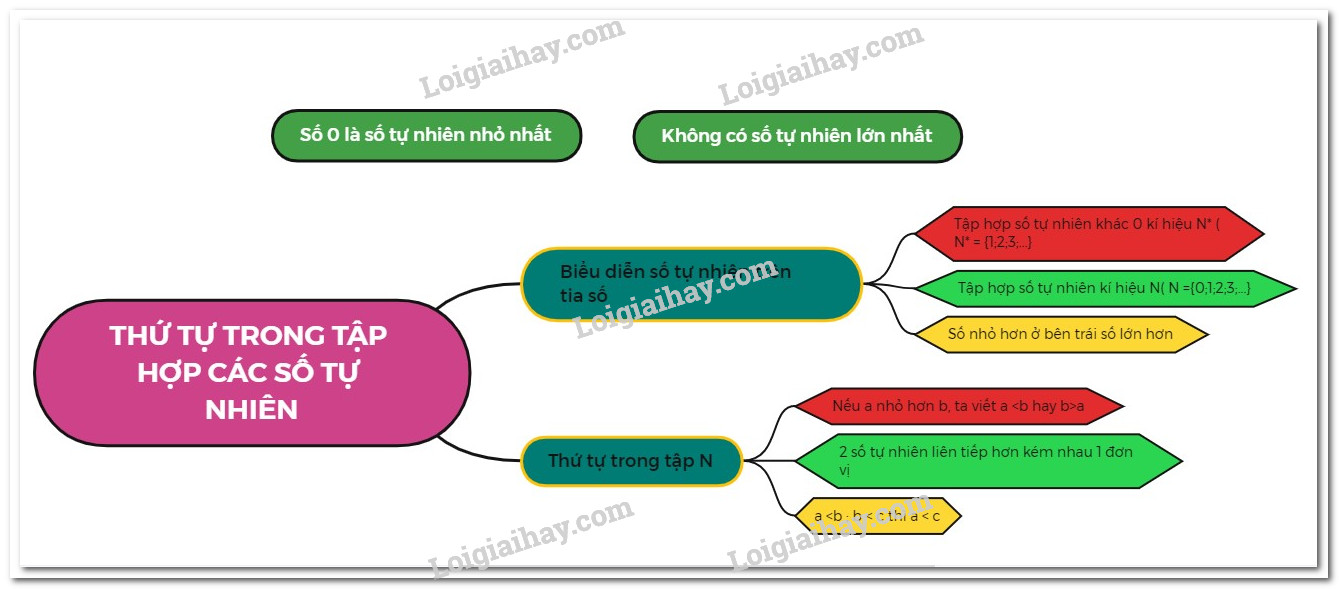
 1. Biểu diễn số tự nhiên trên tia số

Tập hợp các số tự nhiên kí hiệu là \(N\) , tập hợp các số tự nhiên khác 0 kí hiệu là \({N^*}\) .

Ta có:

N = { 0; 1; 2 ; 3 ; 4 ;......}

\({N^*}\)= {1 ; 2 ; 3 ; 4; ......}

Mỗi số tự nhiên được biểu diễn bởi một điểm trên tia số. Trên tia số, điểm biểu diễn số nhỏ ở bên trái điểm biểu diễn số lớn.

Số tự nhiên a được gọi là điểm a. Điểm 0 là gốc.

Ví dụ: Điểm biểu diễn số 4 trên tia số ta gọi là điểm 4.

2. Thứ tự trong tập hợp các số tự nhiên

+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết \(a < b\) hoặc \(b > a.\)

Ngoài ra ta cũng viết \(a \ge b\) để chỉ \(a > b\) hoặc \(a = b.\)

+ Nếu \(a < b\) và \(b < c\) thì \(a < c.\) (Tính chất bắc cầu)

+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất và một số liền trước duy nhất.

+ Số 0 là số tự nhiên bé nhất.

Ví dụ:

Số 3 và số 4 là hai số tự nhiên liên tiếp. Số liền sau của 8 là 9.

Số liền trước của 6 là 5.

Các dạng bài tập

1. Tìm số liền sau, số liền trước của một số tự nhiên cho trước

Phương pháp:

- Để tìm số liền sau của số tự nhiên $a,$ ta tính $a + 1.$

- Để tìm số liền trước của số tự nhiên $a$ khác $0,$ta tính $a - 1.$

 Chú ý:

- Số $0$  không có số liền trước.

- Hai số tự nhiên liên tiếp thì hơn kém nhau $1$  đơn vị.

2. Tìm các số tự nhiên thỏa mãn điều kiện cho trước

Phương pháp:

Liệt kê tất cả các số tự nhiên thỏa mãn đồng thời các điều kiện đã cho

Ví dụ:

Tìm tất cả các số tự nhiên thỏa mãn \(12 < x < 16\)

Giải:

Ta có: các số tự nhiên lớn hơn $12$ và nhỏ hơn $16$ là: $13; 14; 15$.

Tìm tất cả các số tự nhiên thỏa mãn \(12 < x < 16\)

3. Sử dụng công thức đếm số các số tự nhiên

Phương pháp:

 Để đếm các số tự nhiên từ $a$ đến $b,$  hai số liên tiếp cách nhau $d$  đơn vị, ta dùng công thức sau:

$\dfrac{{b - a}}{d} + 1$ hay bằng (số cuối – số đầu):khoảng cách +1.

- Căn cứ vào các phần tử đã được liệt kê hoặc căn cứ vào tính chất đặc trưng cho các phần tử của tập hợp cho trước, ta có thể tìm được số phần tử của tập hợp đó.

- Sử dụng các công thức sau:

+ Tập hợp các số tự nhiên từ $a$ đến $b$ có: $b-a + 1$ phần tử  (1)

+ Tập hợp các số chẵn từ số chẵn $a$ đến số chẵn $b$ có: $\left( {b-a} \right):2 + 1$ phần tử  ( 2)

+ Tập hợp các số lẻ từ số lẻ $m$ đến số lẻ $n$ có: $\left( {n - m} \right):2 + 1$ phần tử  ( 3)

+ Tập hợp các số tự nhiên từ $a$  đến $b,$  hai số kế tiếp cách nhau d đơn vị, có: $\left( {b - a} \right):d + 1$ phần tử  (4)