Lý thuyết phương trình đường tròn

1. Lập phương trình đường tròn có tâm và bán kính cho trước

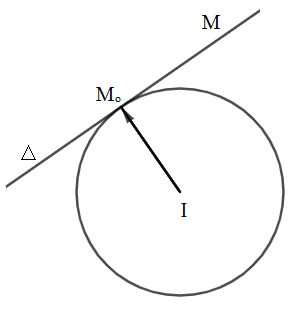
Phương trình đường tròn có tâm \(I(a; b)\), bán kính \(R\) là :

$${(x - a)^2} + {(y - b)^2} = {R^2}$$

2. Nhận xét

Phương trình đường tròn  \({(x - a)^2} + {(y - b)^2} = {R^2}\)  có thể được viết dưới dạng 

$${x^2} + {y^2} - 2ax - 2by + c = 0$$

trong đó \(c = {a^2} + {b^2} - {R^2}\)

\( \Rightarrow \) Điều kiện để phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình đường tròn \((C)\) là: \({a^2} + {b^2}-c>0\). Khi đó, đường tròn \((C)\) có tâm \(I(a; b)\) và bán kính \(R = \sqrt{a^{2}+b^{2} - c}\)

3. Phương trình tiếp tuyến của đường tròn

Cho điểm \({M_0}({x_0};{y_0})\) nằm trên đường tròn \((C)\) tâm  \(I(a; b)\).Gọi \(∆\) là tiếp tuyến với \((C)\) tại \(M_0\)

Ta có \(M_0\) thuộc \(∆\) và vectơ \(\vec{IM_{0}}=({x_0} - a;{y_0} - b)\) là vectơ  pháp tuyến cuả \( ∆\)

Do đó  \(∆\) có phương trình là:

$({x_0} - a)(x - {x_0}) + ({y_0} - b)(y - {y_0}) = 0$      (1)

Phương trình (1) là phương trình tiếp tuyến của đường tròn \({(x - a)^2} + {(y - b)^2} = {R^2}\)  tại điểm \(M_0\) nằm trên đường tròn.

4. Bài tập về phương trình đường tròn

Bài 1: Cho đường cong (C_m): x²+y²-2mx-4(m-2)y+6-m=0. Tìm điều kiện của m để (C_m) là phương trình đường tròn.

Lời giải: 

Điều kiện để \((C_m)\) là phương trình đường tròn là:

\(\eqalign{
& {a^2} + {b^2} - c > 0 \Leftrightarrow {m^2} + 4{\left( {m - 2} \right)^2} - \left( {6 - m} \right) > 0 \cr
& \Leftrightarrow 5{m^2} - 15m + 10 > 0 \Leftrightarrow \left[ \matrix{
m > 2 \hfill \cr
m < 1 \hfill \cr} \right. \cr} \)

Bài 2: Viết phương trình của đường tròn có tâm \(I\left( -3;4 \right)\)và bán kính \(R=2\)

Lời giải:

Phương trình của đường tròn có tâm \(I(-3;4)\) và bán kính \(R=2\) là: \({{(x+3)}^{2}}+{{(y-4)}^{2}}={{2}^{2}}\) hay\({{(x+3)}^{2}}+{{(y-4)}^{2}}-4=0\)

Bài 3: Phương trình nào sau đây là phương trình đường tròn?

A. \({{x}^{2}}+2{{y}^{2}}-4x-8y+1=0\)

B. \(4{{x}^{2}}+{{y}^{2}}-10x-6y-2=0\)

C. \({{x}^{2}}+{{y}^{2}}-2x-8y+20=0\)                                     

D. \({{x}^{2}}+{{y}^{2}}-4x+6y-12=0\)

Lời giải: 

\({{x}^{2}}+2{{y}^{2}}-4x-8y+1=0\) không phải là phương trình đường tròn. Vì \({{x}^{2}}:{{y}^{2}}=1:2\ne 1:2\) 

\(4{{x}^{2}}+{{y}^{2}}-10x-6y-2=0\) không phải là phương trình đường tròn. Vì \({{x}^{2}}:{{y}^{2}}=4:1\ne 1:2\)

\({{x}^{2}}+{{y}^{2}}-2x-8y+20=0\)có \(a=1\,\,,b=4,\,\,c=20\). Ta thấy \(a,b,c\)không thỏa mãn điều kiện \({{a}^{2}}+{{b}^{2}}>c\). Đây không phải là một phương trình đường tròn. 

\({{x}^{2}}+{{y}^{2}}-4x+6y-12=0\) có \(a=2,\,\,b=-3,\,\,c=-12\). Ta thấy \(a,b,c\) thỏa mãn điều kiện \({{a}^{2}}+{{b}^{2}}>c\). Đây là một phương trình đường tròn.

Bài 4: Phương trình \({{x}^{2}}+{{y}^{2}}-2x+4y+1=0\)  là phương trình của đường tròn nào?

Lời giải:

\({{x}^{2}}+{{y}^{2}}-2x+4y+1=0\) có hệ số \(a=1,b=-2,c=2\)  sẽ có tâm \(I\left( 1;-2 \right)\) và \(R=\sqrt{{{\left( -1 \right)}^{2}}+{{2}^{2}}-1}=2\)

Bài 5: Trong số các đường tròn có phương trình dưới đây, đường tròn nào đi qua gốc tọa độ\(O(0,0)\)?

A. \({{x}^{2}}+{{y}^{2}}=1.\) 

B.  \({{x}^{2}}+{{y}^{2}}-x-y+2=0\)

C. \({{x}^{2}}+{{y}^{2}}-4x-4y+8=0.\)

D.  \({{(x-3)}^{2}}+{{(y-4)}^{2}}=25.\)

Lời giải: 

A. \({{x}^{2}}+{{y}^{2}}=1.\) Thay \(x=0,y=0\) ta có \({{0}^{2}}+{{0}^{2}}=2\) là mệnh đề sai.

B. \({{x}^{2}}+{{y}^{2}}-x-y+2=0\). Thay \(x=0,y=0\) ta có \(2=0\) là mệnh đề sai.

C. \({{x}^{2}}+{{y}^{2}}-4x-4y+8=0.\) Thay \(x=0,y=0\) ta có \(8=0\) là mệnh đề sai.

D. \({{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=25.\) Thay \(x=0,y=0\) ta có \({{\left( -3 \right)}^{2}}+{{\left( -4 \right)}^{2}}=25\) là mệnh đề đúng. Vậy \({{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=25.\) đi qua gốc tọa độ.

Bài 6: Viết phương trình đường tròn (C) có tâm \(I(2;-4)\)  và đi qua điểm \(A(1;3)\) 

Lời giải:

Ta có: \(R=IA=\sqrt{{{\left( 1-2 \right)}^{2}}+{{\left( 3+4 \right)}^{2}}}=\sqrt{50}\)

Phương trình đường tròn (C) có tâm \(I\left( 2;-4 \right)\)có bán kính \(R=\sqrt{50}\) là: \({{\left( x-2 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=50.\)

Bài 7: Xác định mối quan hệ giữa điểm \(M(4;2)\)  và đường tròn \((C)\)  có phương trình \({{x}^{2}}+{{y}^{2}}-8x-6y+21=0\)

Lời giải:

Đường tròn \(\left( C \right)\) có phương trình \({{x}^{2}}+{{y}^{2}}-8x-6y+21=0\) sẽ có tâm \(I\left( 4;3 \right)\) bán kính \(R=\sqrt{{{4}^{2}}+{{3}^{2}}-21}=2\).

Ta có \(MI=\sqrt{{{\left( 4-4 \right)}^{2}}+{{\left( 2-3 \right)}^{2}}}=1<R=2\Rightarrow M\) nằm trong \(\left( C \right)\)

Bài 8: Viết phương trình đường tròn (C) có tâm \(O\left( 0;0 \right)\)  và đi qua điểm \(A(1;3)\)

Lời giải:

Ta có \(R=OA=\sqrt{{{\left( 1-0 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}=\sqrt{10}\)

Phương trình đường tròn (C) có tâm \(O\left( 0;0 \right)\) có bán kính \(R=\sqrt{10}\) là: \({{x}^{2}}+{{y}^{2}}=10.\)

Bài 9: Viết phương trình đường tròn tâm I thuộc đường thẳng d có phương trình\(x-2y+5=0\)  và đi qua hai điểm\(A\left( 0;4 \right),\,B\left( 2;6 \right)\)

Lời giải:

Giả sử điểm \(I\left( {{x}_{I}};{{y}_{I}} \right)\) là tâm của đường tròn (C). Vì I nằm trên đường thẳng \(x-2y+5=0\) nên ta có \({{x}_{I}}-2{{y}_{I}}+5=0\,\,\,\,\,\left( 1 \right)\)

Vì đường tròn (C) đi qua hai điểm \(A\left( 0;4 \right),\,\,B\left( 2;6 \right)\) nên ta có \(IA=IB\). Điều này tương đương với \(I{{A}^{2}}=I{{B}^{2}}\)  hay \({{\left( {{x}_{I}} \right)}^{2}}+{{\left( 4-{{y}_{I}} \right)}^{2}}={{\left( 2-{{x}_{I}} \right)}^{2}}+{{\left( 6-{{y}_{I}} \right)}^{2}}\Leftrightarrow {{x}_{I}}+{{y}_{I}}-6=0\,\,\,\left( 2 \right)\)

.Từ (1) và (2) suy ra \(\left\{ \begin{array}{l}{x_I} - 2{y_I} + 5 = 0\\{x_I} + {y_I} - 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \frac{7}{3}\\{y_I} = \frac{{11}}{3}\end{array} \right. \Rightarrow I\left( {\frac{7}{3};\frac{{11}}{3}} \right)\).

Mặt khác ta có \(R=IA=\sqrt{{{\left( \frac{7}{3} \right)}^{2}}+{{\left( \frac{11}{3}-4 \right)}^{2}}}=\sqrt{\frac{50}{9}}\) 

Vậy (C) có dạng \(\left( C \right):{{\left( x-\frac{7}{3} \right)}^{2}}+{{\left( y-\frac{11}{3} \right)}^{2}}=\frac{50}{9}\)

Bài 10: Viết phương trình đường tròn (C) đi qua 3 điểm \(A(1;4),B(-4;0)\) và \(C(-2;2)\)

Lời giải:

Phương trình đường tròn đi qua 3 điểm là: \({{x}^{2}}+{{y}^{2}}-17x+21y-84=0\)