Lý thuyết hàm số lũy thừa

1. Khái niệm hàm số lũy thừa

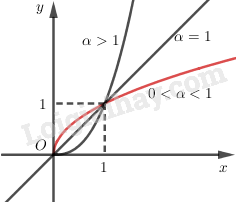
Hàm số lũy thừa là các hàm số dạng $y = {x^\alpha }\left( {\alpha  \in R} \right)$. Các hàm số lũy thừa có tập xác định khác nhau, tùy theo $\alpha$: 

- Nếu $\alpha$ nguyên dương thì tập các định là $R$.

- Nếu $\alpha$ nguyên âm hoặc $\alpha  = 0$ thì tập các định là $R\backslash \left\{ 0 \right\}$.

- Nếu $\alpha$ không nguyên thì tập các định là $\left( {0; + \infty } \right)$.

Chú ý: Hàm số $y = \sqrt x$ có tập xác định là $\left[ {0; + \infty } \right)$, hàm số $y = \sqrt[3]{x}$ có tập xác định $R$, trong khi đó các hàm $y = {x^{\frac{1}{2}}},y = {x^{\frac{1}{3}}}$ đều có tập xác định $(0; +∞)$. Vì vậy $y = \sqrt x$ và $y = {x^{\frac{1}{2}}}$ ( hay $y = \sqrt[3]{x}$ và $y = {x^{\frac{1}{3}}}$) là những hàm số khác nhau.

2. Đạo hàm của hàm số lũy thừa với số mũ tổng quát 

- Hàm số $y = {x^\alpha }$ có đạo hàm tai mọi $x ∈ (0; +∞)$ và $y' = \left( {{x^\alpha }} \right)' = \alpha {x^{\alpha  - 1}}$

- Nếu hàm số $u=u(x)$ nhận giá trị dương và có đạo hàm trong khoảng $J$ thì hàm số $y = {u^\alpha }\left( x \right)$ cũng có đạo hàm trên $J$ và $$y' = \left[ {{u^\alpha }\left( x \right)} \right]' = \alpha {u^{\alpha  - 1}}\left( x \right)u'\left( x \right)$$

3. Đạo hàm của hàm số lũy thừa với số mũ nguyên dương

Trong trường hợp số mũ nguyên dương, hàm số lũy thừa $y=x^n$ có tập xác định là $R$ và có đạo hàm trên toàn trục số. Công thức tính đạo hàm số lũy thừa tổng quát được mở rộng thành $\forall x \in R,\left( {{x^n}} \right)' = n{x^{n - 1}}$ và $$\forall x \in J,\left[ {{u^n}\left( x \right)} \right]' = n{u^{n - 1}}\left( x \right)u'\left( x \right)$$  nếu $u= u(x)$ có đạo hàm trong khoảng $J$.

4. Đạo hàm của hàm số  lũy thừa với số mũ nguyên âm

Nếu số mũ là số nguyên âm thì hàm số lũy thừa $y=x^n$ có tập xác định là $R\backslash \left\{ 0 \right\}$ và có đạo hàm tại mọi $x$ khác $0$, công thức đạo hàm hàm số lũy thừa tổng quát được mở rộng thành $\forall x \ne 0,\left( {{x^n}} \right)' = n{x^{n - 1}}$ và  $$\forall x \in J,\left[ {{u^n}\left( x \right)} \right]' = n{u^{n - 1}}\left( x \right)u'\left( x \right)$$

nếu $u= u(x) \ne 0$ có đạo hàm trong khoảng $J$.

5. Đạo hàm của căn thức

Hàm số $y = \sqrt[n]{x}$ có thể xem là mở rộng của hàm lũy thừa $y = {x^{\frac{1}{n}}}$ (tập xác định của $y = \sqrt[n]{x}$ chứa tập xác định của $y = {x^{\frac{1}{n}}}$ và trên tập xác định của $y = {x^{\frac{1}{n}}}$ thì hai hàm số trùng nhau).

Khi $n$ lẻ thì hàm số $y = \sqrt[n]{x}$ có tập xác định $R$. Trên khoảng $(0; +∞)$ ta có $y = \sqrt[n]{x} = {x^{\frac{1}{n}}}$ và $\left( {{x^{\frac{1}{n}}}} \right)' = \dfrac{1}{n}{x^{\frac{1}{n} - 1}}$, do đó $\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}$.

Công thức này còn đúng cả với $x < 0$ và hàm số $y = \sqrt[n]{x}$ không có đạo hàm tại $x= 0$.

Khi $n$ chẵn hàm $y = \sqrt[n]{x}$ có tập xác định là $[0;+∞)$, không có đạo hàm tại $x= 0$ và có đạo hàm tại mọi $x > 0$ tính theo công thức:

$$\left( {\sqrt[n]{x}} \right)' =\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}$$

Tóm lại, ta có $\left( {\sqrt[n]{x}} \right)' =\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}$ đúng với mọi $x$ làm cho hai vế có nghĩa.

Sử dụng quy tắc đạo hàm hàm hợp ta suy ra: Nếu $u=u(x)$ là hàm có đạo hàm trên khoảng $J$ và thỏa mãn điều kiện $u(x) > 0, ∀x ∈ J$ khi $n$ chẵn, $u\left( x \right) \ne 0,\forall x \in J$ khi $n$ lẻ thì

$$\forall x \in J,\left( {\sqrt[n]{{u\left( x \right)}}} \right)' = \dfrac{{u'\left( x \right)}}{{n\sqrt[n]{{{u^{n - 1}}\left( x \right)}}}}$$

6. Đồ thị hàm số $y = {x^\alpha }$ trên khoảng $(0; +∞)$

Chú ý: Khi khảo sát hàm số $y = {x^\alpha }$ với $\alpha$ cụ thể, cần xét hàm số trên toàn tập xác định của nó (chứ không phải chỉ xét trên khoảng $(0; +∞)$ như trên).

Loigiaihay.com