Lý thuyết Giao thoa sóng - Vật Lí 11 Cánh diềuSự giao thoa của hai sóng mặt nước Giao thoa ánh sáng Quảng cáo
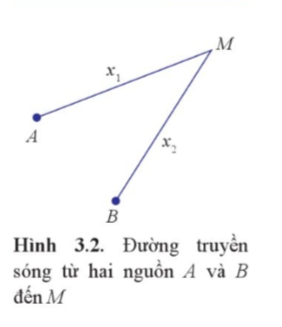
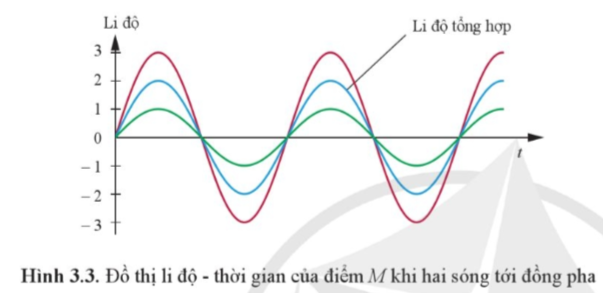
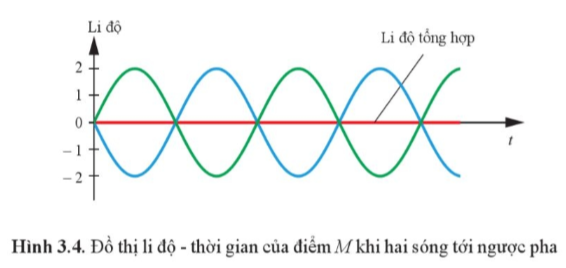
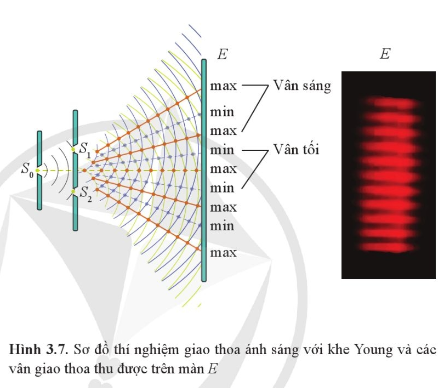
BÀI 3. GIAO THOA SÓNG I. Sự giao thoa của hai sóng mặt nước Sự tạo thành vân giao thoa - Giả sử A và B là hai nguồn dao động cùng phương, cùng tần số và cùng pha. Sóng do hai nguồn tạo ra cùng truyền đến điểm M ở cách A và B các khoảng lần lượt là x1 và x2 - Những điểm dao động với biên độ lớn nhất là những điểm mà hiệu đường đi của sóng từ hai nguồn đến đó là \({x_2} - {x_1} = k\lambda \) (k là số nguyên) - Những điểm dao động với biên độ nhỏ nhất là những điểm mà hiệu đường đi của sóng từ hai nguồn đến đó là \({x_2} - {x_1} = (k + \frac{1}{2})\lambda \) (k là số nguyên) - Tổng hợp các điểm dao động với biên độ lớn nhất hoặc dao động với biên độ nhỏ nhất tạo thành các đường xác định trong vùng giao nhau của hai sóng được gọi là hệ vân giao thoa của hai sóng - Hai nguồn kết hợp là hai nguồn dao động cùng phương, cùng tần số và có độ lệch pha không đổi theo thời gian - Hai sóng do hai nguồn kết hợp tạo ra là hai sóng kết hợp - Hiện tượng hai sóng kết hợp, khi gặp nhau tại những điểm xác định, luôn luôn hoặc làm tăng cường, hoặc làm yếu nhau được gọi là hiện tượng giao thoa của sóng - Điều kiện để có hiện tượng giao thoa sóng là hai sóng phải xuất phát từ hai nguồn dao động có cùng tần số, cùng phương dao động và có độ lệch pha không đổi theo thời gian - Hiện tượng giao thoa là hiện tượng đặc trưng của sóng II. Giao thoa ánh sáng - Hiện tượng giao thoa ánh sáng là hiện tượng xuất hiện các vạch sáng xen kẽ với các vạch tối khi hai sóng ánh sáng kết hợp gặp nhau - Khoảng cách giữa hai vân sáng (hoặc hai vân tối) liên tiếp được gọi là khoảng vân, kí hiệu là i \(i = \frac{{\lambda D}}{a}\) - Khoảng cách từ vân sáng thứ k đến vân sáng trung tâm được tính bằng \({x_s} = ki\) - Khoảng cách từ vân tối thứ k đến vân sáng trung tâm được tính bằng \({x_t} = (k - \frac{1}{2})i\) Sơ đồ tư duy về “Giao thoa sóng” |























Danh sách bình luận