Lý thuyết Đồ thị hàm số bậc nhất y = ax + b ( a ≠ 0) SGK Toán 8 - Cánh diềuĐồ thị của hàm số bậc nhất là gì? Quảng cáo
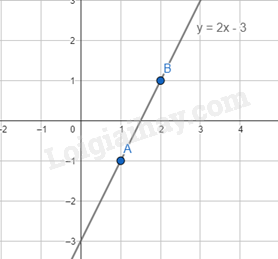
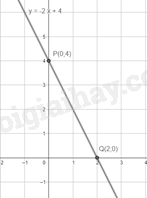
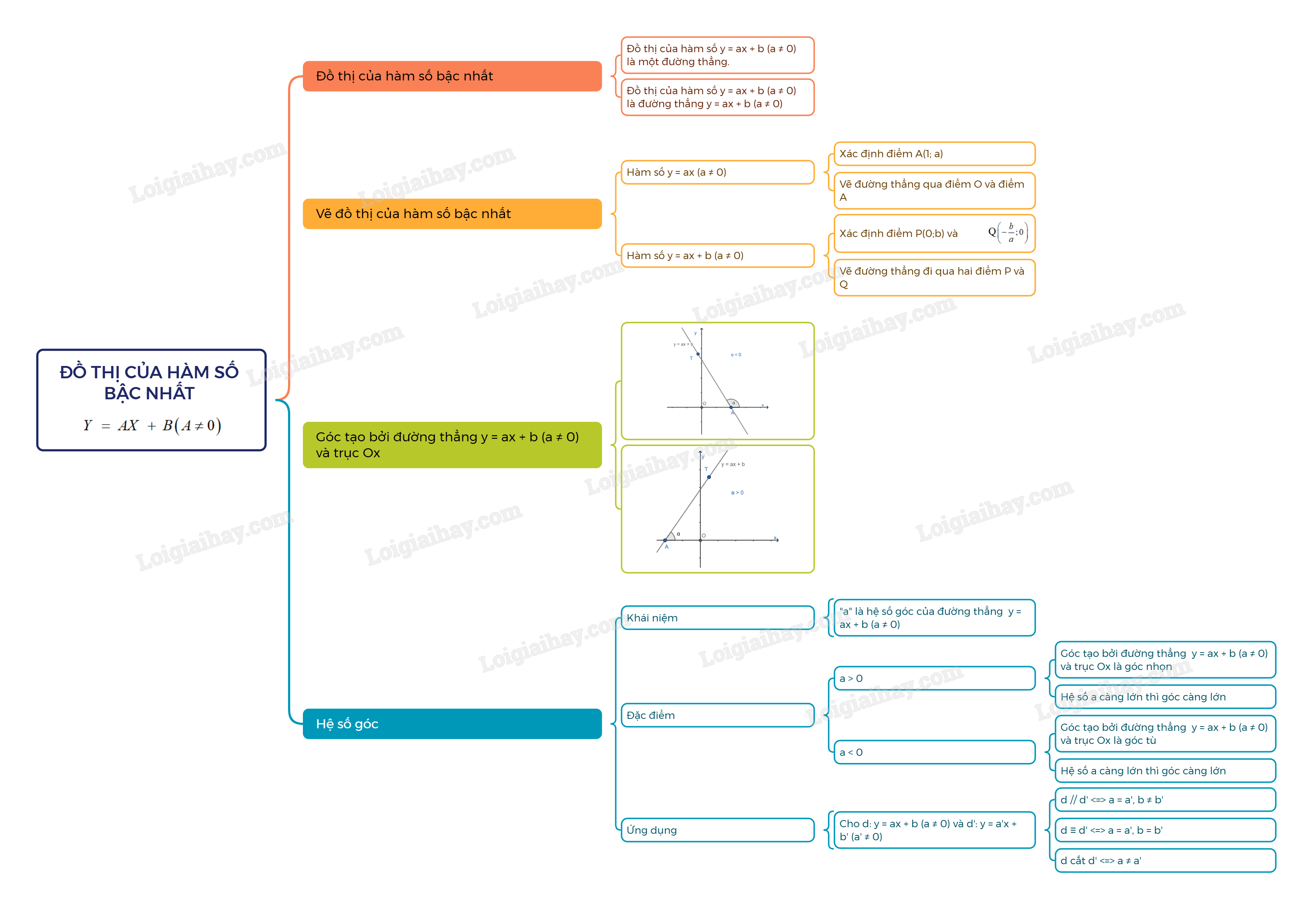
1. Đồ thị của hàm số bậc nhất Đồ thị của hàm số y = ax + b (a\( \ne \)0) là một đường thẳng. Chú ý: Đồ thị hàm số y = ax + b (a\( \ne \)0) còn gọi là đường thẳng y = ax + b (a\( \ne \)0). Ví dụ: Cho hàm số y = 2x – 3 có hai điểm A(1, -1) và B(2; 1) thuộc đồ thị của hàm số y = 2x – 3. 2. Vẽ đồ thị của hàm số bậc nhất Hàm số y = ax (a\( \ne \)0) Để vẽ đồ thị của hàm số y = ax (a\( \ne \)0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A. Hàm số y = ax + b (a\( \ne \)0) Để vẽ đồ thị của hàm số y = ax + b (a\( \ne \)0, b\( \ne \)0), ta có thể xác định hai điểm P(0; b) và Q\(\left( { - \frac{b}{a};0} \right)\) rồi vẽ dường thẳng đi qua hai điểm đó. Ví dụ: Cho hàm số y = -2x + 4 Với x = 0 thì y = 4, ta được điểm P(0;4) Với y = 0 thì x = 22, ta được điểm Q(2;0) Vậy đồ thị hàm số y = -2x + 4 là đường thẳng đi qua hai điểm P(0;4) và Q(2;0)
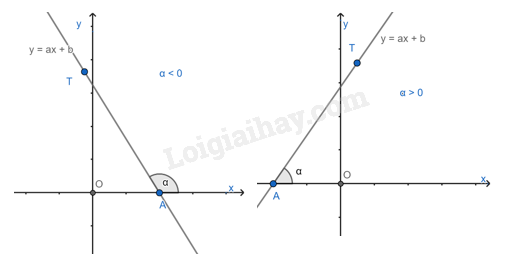
3. Hệ số góc của đường thẳng y = ax + b (a\( \ne \)0) Góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox. Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a\( \ne \)0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương. Góc \(\alpha \) tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc \(\alpha \))
Hệ số góc Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a\( \ne \)0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a\( \ne \)0). Nhận xét: Khi hệ số góc a > 0 thì góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn. Khi hệ số góc a < 0 thì góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn. Ứng dụng của hệ số góc Cho d: y = ax + b (a\( \ne \)0) và d’: y = a’x + b’ (a’\( \ne \)0) a. d // d’ \( \Leftrightarrow \) a = a’, b \( \ne \)b’. b.\(d \equiv d' \Leftrightarrow a = a',b = b'\) c. d cắt d’ \( \Leftrightarrow \) a \( \ne \)a’ Ví dụ: y = 2x + 1, y = 2x + 3 là hai đường thẳng song song vì có hệ số góc bằng nhau và hệ số tự do khác nhau.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
