Lý thuyết Dấu hiệu chia hết cho 3, cho 9 Toán 6 Cánh diềuLý thuyết Dấu hiệu chia hết cho 3, cho 9 Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu Quảng cáo
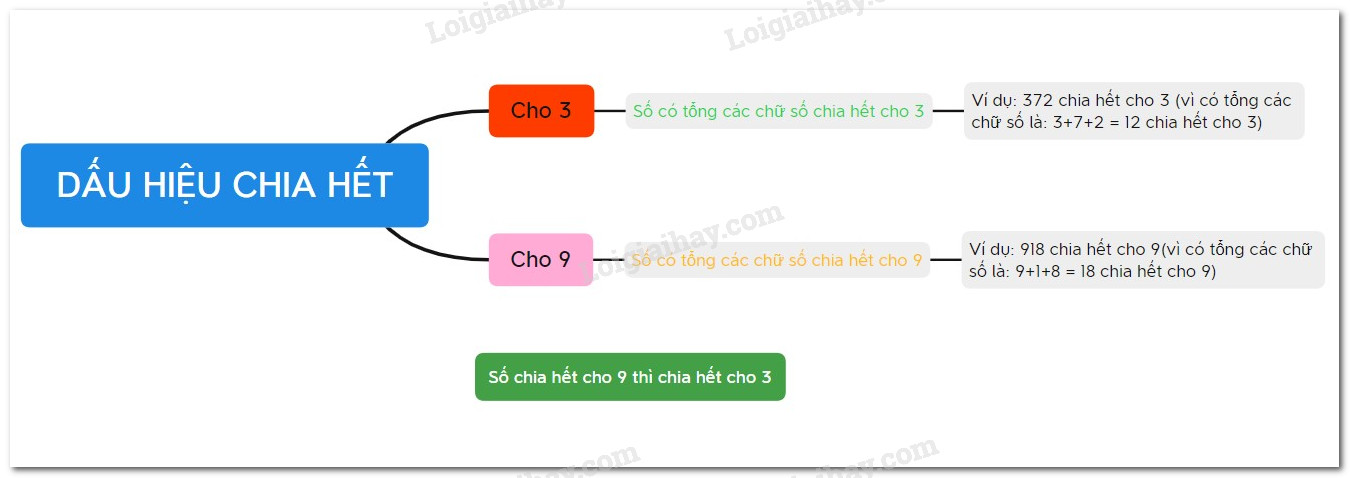
I. Dấu hiệu chia hết cho 9 Dấu hiệu: Các số có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9 và chỉ những số đó chia hết cho 9. Ví dụ: a) Số $1944$ chia hết cho $9$ vì có tổng các chữ số là $1+9+4+4=18$ chia hết cho $9$. b) Số $7325$ không chia hết cho $9$ vì có tổng các chữ số là $7+3+2+5=17$ không chia hết cho $9$. II. Dấu hiệu chia hết cho 3Dấu hiệu: Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó chia hết cho 3. Ví dụ: a) Số $90156$ chia hết cho $3$ vì có tổng các chữ số là $9+0+1+5+6=21$ chia hết cho $3$. b) Số $6116$ không chia hết cho $3$ vì có tổng các chữ số là $6+1+1+6=14$ không chia hết cho $3$. Lưu ý: - Một số chia hết cho 9 thì sẽ chia hết cho 3. - Một số chia hết cho 3 chưa chắc đã chia hết cho 9 Chẳng hạn: Số 6 chia hết cho 3 nhưng 6 không chia hết cho 9. CÁC DẠNG TOÁN VỀ DẤU HIỆU CHIA HẾT CHO 3, CHO 9I. Nhận biết các số chia hết cho 9Phương pháp giải Sử dụng dấu hiệu chia hết cho cho 9. Sử dụng tính chất chia hết của tổng, của hiệu. Ví dụ: 100984 có tổng các chữ số là: 1+9+8+4=22 22 là số không chia hết cho 9 nên 100984 không chia hết cho 9 13545 có tổng các chữ số là: 1+3+5+4+5=18. Số 18 chia hết cho 9 nên 13545 chia hết cho 9. II. Viết các số chia hết cho 9 từ các số hoặc các chữ số cho trướcPhương pháp Các số chia hết cho 9 là các số có tổng các chữ số chia hết cho 9. Ví dụ: Cho \(\overline {1a32} \) chia hết cho 9. Tìm số thay thế cho \(a\). Giải: Tổng các chữ số của \(\overline {1a32} \) là \(1 + a +3 + 2 = a + 6\) để số \(\overline {1a32} \) chia hết cho 9 thì \(a + 6\) phải chia hết cho 9. Do $a$ là các số tự nhiên từ 0 đến 9 nên \(\begin{array}{l}0 + 6 \le a +6 \le 9 + 6\\ \Rightarrow 6 \le a + 6 \le 15\end{array}\) Số chia hết cho 9 từ 6 đến 15 chỉ có đúng một số 9, do đó \(a +6 = 9 \Rightarrow a = 3\) Vậy số thay thế cho a chỉ có thể là 3. III. Bài toán có liên quan đến số dư trong phép chia một số tự nhiên cho 9Phương pháp giải - Sử dụng tính chất: Số dư của một số khi chia cho $9$ bằng số dư của tổng các chữ số của số đó khi chia cho $9$. Ví dụ: ho số \(N = \overline {5a} \). Tìm các số tự nhiên $N$ sao cho $N$ chia cho $9$ dư $5$. Giải: Vì $N$ chia cho $9$ dư $5$ nên $a+5$ chia cho $9$ dư $5$. => $a$ chia hết cho $9$. Mà \(a \in \left\{ {0;\,\,1;\,\,2;\,\,.......;\,\,9} \right\}\) =>$a$ chỉ có thể là $0;9$ => $N$ có thể là $50;59$ IV. Nhận biết các số chia hết cho 3Phương pháp Sử dụng dấu hiệu chia hết cho 3. Sử dụng tính chất chia hết của tổng, của hiệu. Ví dụ: a) 555464 có tổng các chữ số là: 5+5+5+4+6+4=29 không chia hết cho 3 nên 555464 không chia hết cho 3. b) 15645 có tổng các chữ số là: 1+5+6+4+5=21 chia hết cho 3 nên 15645 chia hết cho 3. V. Viết các số chia hết cho 3 từ các số hoặc các chữ số cho trướcPhương pháp giải Các số chia hết cho 3 là các số có tổng các chữ số chia hết cho 3. Ví dụ: Cho \(\overline {1a3} \) chia hết cho 3. Tìm số thay thế cho \(a\). Giải: Tổng các chữ số của \(\overline {1a3} \) là \(1 + a +3 = a + 4\) để số \(\overline {1a3} \) chia hết cho 3 thì \(a + 4\) phải chia hết cho 3. Do $a$ là các số tự nhiên từ 0 đến 9 nên \(\begin{array}{l}0 + 4 \le a +4 \le 9 +4\\ \Rightarrow 4 \le a + 4 \le 13\end{array}\) Số chia hết cho 3 từ 4 đến 13 có 3 số lần lượt là 6, 9, 12. Với \(a +4 = 6 \Rightarrow a = 2\). Với \(a +4 = 9 \Rightarrow a = 5\) Với \(a +4 = 12 \Rightarrow a = 8\) Vậy số thay thế cho a có thể là 2, 5, 8. VI. Bài toán có liên quan đến số dư trong phép chia một số tự nhiên cho 3Phương pháp - Số dư trong phép chia cho 3 chỉ có thể là 0, 1 hoặc 2. - Mọi số tự nhiên $n$ luôn có thể được viết một trong 3 dạng sau: +) Dạng 1: $n=3k$ (số chia hết cho 3); +) Dạng 2: $n=3k+1$ (số chia cho 3 dư 1); +) Dạng 3: $n=3k+2$ (số chia cho 3 dư 2) Với $k\in \mathbb{Z}$. Ví dụ: Cho số \(N = \overline {5a} \). Tìm các số tự nhiên $N$ sao cho $N$ chia cho $3$ dư $2$. Giải: \(N = \overline {5a} =50+a\) Vì $N$ chia cho $3$ dư $2$ nên $N-2$ chia hết cho $3$. => $50+a-2$ chia hết cho $3$. => $a+48$ chia hết cho $3$. Vì $48$ chia hết cho $3$ nên để tổng $a+48$ chia hết cho $3$ thì $a$ cũng phải chia chết cho $3$. Mà \(a \in \left\{ {0;\,\,1;\,\,2;\,\,.......;\,\,9} \right\}\) =>$a$ chỉ có thể là $0;3;6;9$ => $N$ có thể là $50;53;56;59$
|




















Danh sách bình luận